N	Titolo	Gioco	Fonte	Soluzione
1	IL RESTO	Un arabo, morendo, lasciò i suoi beni a tre nipoti, con la disposizione che il maggiore ne avesse la metà, il secondo la terza parte e l'ultimo la nona parte. Poiché la fortuna lasciata dall'arabo consisteva in 17 cammelli, nacquero subito feroci discussioni fra gli eredi. Stanchi, alfine, di litigare i tre si affidarono al giudizio di un vecchio e saggio sceicco. "Ero amico del vostro defunto zio e non guarderò a sacrifici pur di esaudire le sue ultime volontà" egli disse. "Prendete, dunque, il mio cammello e unitelo ai vostri ; così ne avrete 18". "La metà di 18 è 9, un terzo di 18 è 6 e un nono di 18 è 2", aggiunse quando i 18 cammelli furono riuniti. "Prendete, quindi, tu 9, tu 6 e tu 2 cammelli e andatevene in pace. Ma, prima, fatemi il piacere di ricondurre alla mia tenda il mio cammello che, per fortuna, è avanzato, dato che 9 + 6 + 2 è uguale a 17". La faccenda sembra veramente inspiegabile a chi non rifletta che il testamento dell'arabo era sbagliato alla radice. Infatti 1/2 +1/3 + 1/9 = 9/18 + 6/18 + 2/18 = 17/18 mentre la somma delle parti avrebbe dovuto essere uguale a 18/18 o a 17/17 (cioè uguale ad 1), come avviene in ogni ripartizione sensata. Nel nostro caso un diciottesimo dell'eredità non era stato attribuito a nessuno. Ciò consentì all'astuto sceicco di dare ad ogni erede più di quanto gli sarebbe spettato, senza rimetterci nulla.	Storiella è di origine araba. Essa fa il giro del mondo (e dei libri di aritmetica) da molti secoli; ma tu, forse, troverai qualche amico che ancora non la conosce e potrai divertirti a metterlo in imbarazzo. Ecco di cosa si tratta.
2	LE CENTO LAMPADINE	Hai cento lampadine, tutte in fila e tutte spente, numerate da 1 a 100. Parti dalla prima lampadina e cambi lo stato di tutte le lampadine (in questo caso le accendi tutte). Poi vai sulla seconda , la quarta la sesta etc... fino a cento e cambi il loro stato. Poi vai sulla terza, la sesta, la nona etc... fino a cento e cambi il loro stato. In pratica aumenti di uno la lampadina da cui parti e cambi lo stato delle lampadine che sono multipli di essa. Così fino ad arrivare alla centesima lampadina (in pratica, alla fine cambi solo la stato della centesima lampadina). Quali saranno alla fine le lampadine che rimarranno accese?
3	IL PROBLEMA DELLE DUE AUTO	Due auto fanno l’andata e il ritorno fra due città distanti 200 chilometri. La prima vettura fa l’andata alla velocità di 50 km/h e il ritorno alla velocità di 40 km/h. La seconda vettura fa l’andata e il ritorno alla velocità media di 45 km/h. Qual è, delle due vetture, quella che mette il minor tempo a effettuare il percorso?		Prima vettura:9 ore. La seconda: 8 ore e 53 minuti
4	LA DIFFERENZA	Qual è il numero di due cifre che diviso per 2, dà per resto 1, diviso per 5, dà per resto 3 diviso per 9, dà per resto 2? (La conoscenza dei resti delle divisioni per 2 e per 5 fanno capire quale è il numero delle unità. La conoscenza del resto della divisione per 9 consente di trovare il numero delle decine)
5	LE DUE FIDANZATE	Giorgio è un bel ragazzo che vive a Monte Nevoso ed ha due fidanzate, una che vive a Colle Fiorito e l'altra che vive a Poggio Ameno. Giorgio vuol bene a tutt'e due e non sa decidersi tanto che quando deve andarle a trovare non sa scegliere da chi andare e lascia decidere al caso; infatti quando arriva alla stazione per prendere il treno prende il primo treno che passa. Sia il treno per Poggio Ameno che quello per Colle Fiorito passano ogni 10 minuti, eppure Giorgio, che esce di casa in orari sempre diversi e casuali, prendendo il primo treno che passa si ritrova 9 volte su 10 a casa della ragazza di Colle Fiorito. Com'è possibile?
6	L'ETÀ DEI FIGLI	Due vecchi matematici che non si vedevano da molto tempo, si incontrano casualmente per strada. Il primo dice di essersi sposato e l'amico gli chiede: "Quanti figli hai?" "Tre. Un maschio e due femmine". "E quanti anni hanno?" "Il prodotto delle loro età, se le consideriamo tutte come numeri interi è 36 e la somma è uguale al numero civico della casa qui di fronte". L'amico riflette un attimo e poi si lamenta: "Non mi hai dato abbastanza elementi!" E il primo precisa: "È vero: la ragazza più grande ha dei bellissimi occhi azzurri!" Quali sono le età dei tre figli?		I tre figli hanno rispettivamente 6, 6 ed 1 anno. Dalla prima informazione si ricava che le possibilità sono: 36 1 1 18 2 1 12 3 1 6 6 1 9 4 1 2 2 9 3 6 2 4 3 3 All'amico non basta sapere la somma. Ciò vuol dire che più combinazioni devono avere lo stesso totale. Le combinazioni con lo stesso totale sono: 6 6 1 2 2 9 Il numero civico visto è infatti il 13, cioè l'unico totale che risulta in più di una possibilità. Sapere il totale sarebbe stato invece sufficiente in tutti gli altri casi. A questo punto, l'informazione finale (c'è un più piccolo) ci fa escludere il caso di due gemelli piccoli.
7	LE DUE PILLOLE	State seguendo una cura delicatissima per una malattia molto rara. Per curarvi dovete prendere tre volte al giorno, alle stesse precise ore, due pillole, una dal flacone A ed una dal flacone B. L'importante è che queste pillole vengano inghiottite insieme, altrimenti se venisse presa una sola di esse gli effetti collaterali sarebbero letali. Ed inoltre se si inghiottissero due pillole dal flacone A o due pillole dal flacone B (invece che una ed una), gli effetti sarebbero ugualmente mortali. Per guarire dalla malattia l'unico metodo è seguire SCRUPOLOSAMENTE la cura che consiste nel finire tutti e due i flaconi, non una pillola di meno, altrimenti non ha effetto la cura. Ed al mondo esistono solo questi due flaconi (la malattia è rarissima). Un giorno, come al solito, versate sulla mano una pillola dal flacone A, e poi fate per versarne una dal flacone B, ma per sbaglio ve ne cadono due. Così adesso vi trovate sulla mano con tre pillole. Il guaio è che le pillole A e B sono assolutamente indistinguibili per forma, colore, peso, odore, etc etc. Non potete gettare via le pillole, perché le pillole sono contate e vi servono tutte. Non potete inghiottirle tutte e tre, pena gravissimi problemi, e non potete chiedere aiuto a nessuno. Ma ce la fate ugualmente. Come avete fatto?		prendere un'altra pillola dal flacone A, mettere le 4 pillole una sopra l'altra (sicuramente sono 2 A e 2 B), e dividere a meta'. Si ottengono due gruppi formati da 4 meta' pillole (2 meta' di A e due meta' di B per ciascuna, cioe' proprio quello che si cercava: due gruppi formati entrambi da una pillola A ed una B). Basterà mangiare uno dei due gruppi, e tenere da parte l'altro gruppo per un'altra occasione.
8	I 20 ORAFI	Uno ricco califfo aveva presso la sua corte 20 orafi che fabbricavano per lui statuette d’oro. Egli forniva a ciascuno di essi delle quantità d’oro con l’accordo che per ogni 100 grammi di oro fornito gli venisse consegnata una statuetta d’oro del peso di 100 grammi. Uno di questi orafi imbrogliava il califfo fabbricando tutte le statuette di 90 grammi. Accortosi dell’inganno, il califfo chiamò il saggio di corte e gli disse: "Devi trovare, potendo utilizzare una bilancia una sola volta, l’orafo che mi imbroglia". Come fece il saggio?
9	TRE CIFRE	Scrivi un qualunque numero intero di tre cifre. Scrivi il numero ottenuto scambiando la la e la 3a cifra del numero considerato. Verifica che la differenza tra il maggiore e il minore dei due numeri che hai scritto è sempre divisibile per 9. Sai giustificare la proprietà sopra enunciata? Se ABC è il minuendo, il sottraendo è CBA, con A > C. Osserva che, nella differenza la cifra delle unità è uguale a 10 + C - A; quella delle decine è 9; quella delle centinaia è A — 1 — C. Dunque, la somma delle cifre della differenza è uguale a 18.
10	3 Compari	Giacomo, Giovanni e Pasquale, vivono nella periferia di un paese, ma ciascuno, per il mestiere che fa, si reca di tanto in tanto in città alla fiera. Un bel giorno, per esser precisi era il primo del mese, capita che i tre amici si incontrano per caso al mercato; contenti di essersi ritrovati decidono di festeggiare a modo loro: dinanzi a un bel boccale di vino. Alla fine, quasi brilli, si ripromettono di rivedersi. Ma con perplessità Giacomo afferma: “ehm…io ci ritornerò ogni tre giorni, ho quindi 1/3 di possibilità di ritrovarmi al mercato, come faremo?”; Giovanni: “ed io ogni quattro giorni, ad essere preciso ho 1/4 di possibilità”; mentre Pasquale afferma che potrà esserci solo ogni cinque giorni, quindi ne avrà sì e no 1/5 di possibilità di ritrovarsi al mercato in un determinato giorno. A questo punto i tre sembrano perplessi: “…e quando allora ci rivedremo, se ciascuno torna in giorni diversi, la probabilità di ritrovarci tutti e tre è praticamente senza speranze!” Esclamò addolorato il buon Pasquale. Ma il trattore, che tra l’altro aveva truffato sul conto, pensò: “accidenti io apro bottega ogni due giorni, mi resta solo il 50% di possibilità di beccarli, ammesso che si incontrino!”, ma dopo appena una frazione di secondo, si illuminò di ingegnosa malizia: “ …ma sì, io lo so quando si ritroveranno, e so anche che sarò qui a fregarli di nuovo!” Come ha potuto l’astuto trattore, pur non disponendo di calendario, in un lampo conoscere con precisione la data dell’incontro dei tre e che in quel giorno di sicuro ci sarebbe stato anche lui?
11	GLI ESPLORATORI E I CAPPELLI	Tre esploratori vengono catturati e condannati a morte avendo però una possibilità di salvarsi. Vengono messi in fila indiana e a ciascuno viene messo in testa un cappello scelto tra cinque: tre bianchi e due neri. In questo modo l’ultimo della fila vede il cappello in testa ai primi due, quello in mezzo vede solo il cappello di quello davanti ed il primo non vede niente. Viene chiesto all’ultimo della fila di indovinare il colore del proprio cappello; questi risponde "non lo so" e viene giustiziato. Tocca quindi a quello in mezzo che, sentita la risposta del suo compagno, risponde anch’egli "non lo so" e viene a sua volta giustiziato. Tocca infine al primo della fila che, sentite le risposte dei compagni, determina con certezza il colore del proprio cappello e si salva. Di che colore era il cappello?		Si supponga che i tre esploratori siano dei logici perfetti, cioè siano in grado di dedurre istantaneamente tutte le conseguenze da un insieme di premesse dato
12	GLI ESPLORATORI E I CAPPELLI	Tre esploratori vengono catturati e condannati a morte avendo però una possibilità di salvarsi. Vengono messi in circolo e a ciascuno viene messo in testa un cappello scelto tra cinque: tre bianchi e due neri. In questo modo ciascuno può vedere il cappello degli altri due ma non il proprio. A questo punto il capo tribù dice: "Farò rullare i tamburi e, al termine, chi sarà certo del colore del proprio cappello potrà dirlo e aver salva la vita". Rullarono i tamburi, ma al termine nessuno parlò. Il capo tribù fece allora rullare i tamburi una seconda volta ma anche questa volta nessuno degli esploratori, magari prudenti ma certo intelligenti, disse nulla. Allora il capo tribù ordinò ai tamburi di rullare ancora, ma stavolta al termine, il più lesto dei tre gridò a gran voce il colore del proprio cappello e si salvò. Di che colore era il cappello?
14	I TRE INTERRUTTORI	Ci troviamo in una stanza; di fronte a noi c'è una porta ermetica chiusa e a fianco 3 interruttori. Solo uno di questi accende la lampadina che c'è nella stanza oltre la porta. Come si può indicare con certezza qul è l'interruttore funzionante potendo entrare nell'altra stanza una sola volta?		Si preme il primo interruttore e si aspetta qualche minuto; si spegne, si preme il secondo interruttore e si entra. Se la lampadina è accesa, l'interruttore funzionante è il secondo. Se è spenta la si tocca: se è calda è il primo, se è fredda è l'ultimo (da focus agosto 2004)
15	I TRE INTERRUTTORI	Fuori da una stanza chiusa, ci sono tre interruttori, uno dei quali comanda una lampadina ad incandescenza che si trova all’interno della stanza; i tre interruttori sono tutti in posizione "spento". Rimanendo fuori dalla stanza e senza la possibilità di sapere cosa accade all’interno, si possono azionare gli interruttori a piacimento; per una volta, e solo una, si può poi entrare nella stanza e fare le verifiche desiderate di ogni tipo. Dopo di ciò, bisognerà uscire dalla stanza ed indicare, con sicurezza, quale dei tre interruttori comanda la lampadina. Come è possibile farlo?	(Grazie a Gianluca Natale per le precisazioni)	Si accende un interruttore e lo si lascia acceso per un po' di tempo. Poi lo si spegne, se ne accende un altro e si entra subito nella stanza. Se la luce è accesa l'interruttore collegato è ovviamente l'ultimo azionato; se la luce è spenta e la lampadina è calda l'interruttore collegato è il primo azionato, che è rimasto acceso per un po'. Diversamente l'interruttore giusto è il terzo che non avete ancora toccato
16	LE LAMPADINE	Immaginiamo di avere una stanza chiusa con tre lampadine al suo interno, a cui sono associati tre interruttori situati all'esterno. Le luci sono tutte spente (situazione di partenza). Io posso entrare solo una volta (e, ovviamente, non posso sbirciare...). Manovrando come credo gli interruttori, devo determinare le associazioni lampadine-interruttori.
17	AL MATH SHOW IL GIOCO SI COMPLICA	I cappelli di tre matematici che partecipano a un gioco televisivo, sono tutti dello stesso colore. Sui tre cappelli viene messe un nastro. Nessuno di loro conosce il colore del nastro che è sul proprio cappello, ma vede il colore dei nastri sui cappelli degli amici e inoltre sa che i nastri disponibili erano due rossi, due gialli e tre verdi. Il conduttore dice: "Due di voi mi sanno dire il colore di un nastro che non sia quello che si trova sul proprio cappello e il terzo, dalle risposte dei suoi compagni, è in grado di dedurre il colore del nastro che si trova sul suo cappello? Se quest'ultimo risponderà esattamente avrete vinto il SuperPremio", Il primo e il secondo matematico confessano di non essere in grado di rispondere. Com'è possibile a questo punto che il terzo matematico deduca il colore del nastro che si trova sul suo cappello?
18	SIAMO NELL'ANNO MILLE	Tre grandi matematici stanno andando a Bagdad, la capitale della matematica. Stanchi per il viaggio, si fermano a riposare sotto un albero. Un ragazzino dispettoso, mentre stanno dormendo, colora i loro cappelli a pallini rossi e gialli. Quando i tre uomini si svegliano vedono i cappelli sulla testa dei loro compagni e scoppiano a ridere. Ma, dopo un po' di tempo, il più intelligente dei tre smette bruscamente di ridere. Perché?
19	LA RISPOSTA DEL PRIGIONIERO	In una tribù selvaggia dell' Africa Centrale esiste l'abitudine di uccidere i prigionieri di guerra dopo averli sottoposti ad un interrogatorio puramente formale. Una INDEROGABILE tradizione però voleva che si impalasse il prigioniero se diceva la verità e che lo si arrostisse se mentiva. Un giorno un prigioniero venne a conoscenza di questa regola e poiché era un furbo matricolato, trovò il modo di sfuggire alla morte. Egli disse semplicemente tre parole; mi sapreste dire quali sono?
20	IL TESORO DIETRO LA PORTA	Ci sono tre porte chiuse, dietro una di esse è nascosto un tesoro e ci viene chiesto di scommettere su una di esse. Ipotizziamo di aver scelto la porta n. 1, lasciando ad un altro le porte n. 2 e n. 3. Supponiamo poi che successivamente venga aperta la porta n. 3 e che dietro di questa non ci sia nulla. Potendo cambiare scelta, conviene puntare sulla porta n. 2, conviene insistere nella scelta iniziale o è indifferente?
21	L’APPRENDISTA STREGONE	Il negromante smise di rimestare la nera pozione che si riscaldava nel calderone e volse lo sguardo in fondo all’oscura caverna a mala pena rischiarata dalla luce delle fiamme che lambivano il pentolone. I riflessi del fuoco trasformavano i suoi occhi in carboni ardenti e creavano sui suoi capelli, lunghi e sbiancati dalla tarda età, strani giochi di luci e colori. Akubens l’apprendista cercò di sostenere quello sguardo e ascoltò le parole del grande negromante. “Akubens, sono anni che mi servi fedelmente ed hai già imparato tutti gli incantesimi e superato tutte le prove… Sei il primo ad esserci riuscito negli ultimi cento anni, ora potrai bere la pozione del potere che ti darà i poteri magici più grandi, potrai comandare sulle cose, sugli animali e sugli uomini, fermare il tempo e guarire tutte le malattie… . Però questa pozione è anche la tua ultima prova. Quando comincerà a bollire la lascerai bollire per 45 minuti esatti poi spegnerai il fuoco, la lascerai raffreddare e ne berrai una coppa. Così il potere sarà tuo. Ma attenzione ! Se la lascerai bollire un minuto in più od in meno la pozione metterà fine alla tua vita e finirai nel regno degli inferi….” -“ Ma, supremo maestro, in questa caverna non ci sono clessidre o altri strumenti per calcolare il tempo e fuori nella fredda notte il cielo è coperto dalle nuvole, è buio e non ci sono le stelle. Come potrò calcolare il tempo?” Il negromante prese qualcosa da una piega del pesante mantello e la gettò ai piedi dell’apprendista: - “Userai queste due corde incatramate, ognuna di esse brucia in un ora esatta” . Così detto con la mano destra disegnò un grande cerchio nell’aria e sparì. Akubens raccolse le due corde incatramate e vide che erano irregolari e di diverso spessore e lunghezza. Si avvicinò al calderone e vide che il calore aumentava, mancava poco tempo. Si mise a pensare agli insegnamenti del sommo maestro e alla fine, quando già la pozione stava cominciando a bollire capì . . . Come ha fatto Akubens a calcolare 45 minuti esatti con solo due corde incatramate da un’ora l’una?	Da “ La vita di Akubens, il più grande stregone della storia” .
22	5 CASE STRANAMENTE ABITATE	Ci sono 5 case di 5 colori differenti e in ogni casa vive una persona di diversa nazionalità. Queste 5 persone bevono una certa bibita, fumano una certa marca di sigarette e hanno un tipo di animale. Nessuno ha lo stesso animale, fuma le stesse sigarette o beve la stessa bibita. Sapendo che: L'inglese vive nella casa rossa. Lo svedese ha cani. Il danese beve tè. La casa verde è a immediatamente a sinistra della bianca. L'abitante della casa verde beve caffè. La persona che fuma Marlboro alleva uccelli. L'abitante della casa gialla fuma Dunhill. L'abitante della casa al centro beve latte. Il Norvegese vive nella prima casa. La persona che fuma Blend vive accanto a quella che ha gatti. La persona che ha cavalli vive accanto a quella che fuma Dunhill. La persona che fuma Camel beve birra. Il tedesco fuma Pall Mall. Il Norvegese vive accanto alla casa blu. La persona che fuma Blend ha un vicino che beve acqua. Sapreste dire con precisione chi ha i pesci?
23	Le 5 case	Dunque: in una strada ci sono cinque case dipinte in cinque colori differenti. In ogni casa vive una persona di differente nazionalità. Ognuno dei padroni di casa beve una differente bevanda, fuma una differente marca di sigarette e tiene un animale differente. Domanda: a chi appartiene il pesciolino? Ecco alcuni indizi: 1) L'inglese vive in una casa rossa. 2) Lo svedese ha un cane. 3) Il danese beve tè. 4) La casa verde è a sinistra della casa bianca. 5) Il padrone della casa verde beve caffé. 6) La persona che fuma le Pall Mall, ha degli uccellini. 7) Il proprietario della casa gialla fuma le Dunhill's. 8) L'uomo che vive nella casa centrale, beve latte. 9) Il norvegese vive nella prima casa. 10) L'uomo che fuma le Blends, vive vicino a quello che ha i gatti. 11) L'uomo che ha i cavalli, vive vicino all'uomo che fuma le Dunhill's. 12) L'uomo che fuma le Blue Master, beve birra. 13) Il tedesco fuma le Prince. 14) Il norvegese vive vicino alla casa blu. 15) L'uomo che fuma le Blends, ha un vicino che beve acqua	Secondo la leggenda, il grande Albert Einstein inventò questo indovinello ed asserì che il 98% della popolazione mondiale non sarebbe stata in grado di risolverlo. Volete cimentarvici per verificare se siete nel restante 2%?	C Giallo            - Blu          - Rossa      - Verde       - Bianca N Norvegese - Danese - Inglese     - Tedesco - Svedese B Acqua          - The          - Latte         - Caffè        - Birra S Dunhill's      - Blends    - Pall-mall - Prince      - Blue mast A Gatti             - Cavalli    - Uccellini   - Pesciolino - Cane Il pesciolino appartiene al tedesco.
24	LA COLAZIONE DEI VIAGGIATORI	Ai tempi dei tempi due Arabi si fermarono in un villaggio per pasteggiare; uno aveva 5 pagnotte e l'altro 3 ma mentre si apprestavano a mangiarle sopravvenne uno straniero che avendo denaro ma non cibo chiese loro di mangiare. Fu convenuto che egli pagò la sua parte; fu diviso il pane in tre parti uguali, lo straniero mangiò e poi pagò 8 monete corrispondenti al valore del pane da lui consumato e se ne andò. L'Arabo che aveva messo in comune le sue cinque pagnotte prese 5 monete e ne lasciò 3 all' altro il quale si infuriò perché ne pretendeva 4 i due litigarono e finirono con l' andare dal giudice. Cosa decise il giudice basandosi esclusivamente sulla logica?
25	LA SPARTIZIONE DEL TESORO	Cinque pirati molto avidi, molto intelligenti e assetati di sangue devono dividersi un bottino di mille dobloni d'oro. I cinque hanno dei nomi particolari legati al loro rango di importanza nel gruppo: Primo è il capo, Secondo il suo vice, seguono - in ordine - Terzo, Quarto e Quinto. Dopo qualche discussione i cinque pirati decidono che ognuno di loro, partendo da colui che si trova più in basso nella scala gerarchica, dovrà fare una proposta di suddivisione del bottino che verrà messa ai voti per l'approvazione. Se la maggioranza, proponente incluso, accetterà, la suddivisione verrà fatta secondo quanto proposto, diversamente colui che ha fatto la proposta verrà ucciso e si passerà ad una nuova proposta. Se voi foste Quinto, che proposta fareste?
26	RAGAZZI AL BAR	Cinque ragazzi vanno al bar e tutti e cinque mangiano e bevono cose diverse. Dalle affermazioni che seguono stabilire che cosa ha mangiato e bevuto ogni ragazzo e che cosa indossava. 1) Uno dei ragazzi beve un'aranciata e mangia un toast. 2) Paolo non beve il suo latte con un biscotto. 3) Marco mangia un panino. 4) Chi beve l'aranciata non indossa la maglia. 5) Chi beve un caffè indossa il gilè. 6) Indossa la giacca chi mangia il biscotto, ma non beve Coca Cola. 7) Ugo indossa il golf e non mangia né toast né brioche. 8) Sergio non indossa il giubbotto. Gli elenchi che seguono non hanno alcun ordine particolare. Ragazzi: Marco, Luca, Ugo, Paolo e Sergio. Cibo: panino, toast, brioche, biscotto e torta. Bevande: aranciata, latte, tè, Coca Cola e caffè. Indumenti: giubbotto, maglia, golf, giacca e gilè.
27	I CAPPELLI DI NONNA MARIA	Un bel mattino nonna Maria decide di fare un regalo ai suoi 6 nipoti, così va al mercato e compra alcuni cappelli. La sera convoca i suoi nipoti, gli fa bendare gli occhi in modo che non possano assolutamente vedere, e dice: "Questa mattina ho comprato 9 cappelli: 2 bianchi, 3 rossi e 4 verdi. Adesso metterò in testa a ciascuno di voi un cappello." Così, dopo aver messo i cappelli in testa ai suoi nipoti, gli leva le bende dagli occhi e dice ad ognuno di loro di indovinare il colore del proprio cappello. Ogni nipote può vedere il colore del cappello degli altri ma non può vedere il proprio e nessuno sa di che colore sono i 3 cappelli rimasti fuori. Passano alcuni minuti ma nessuno parla. La nonna, allora, invita ancora i nipoti a rispondere e così due di loro dicono decisi: "Io ce l'ho verde!" ed indovinano. Poi passano ancora alcuni minuti senza che nessuno dice niente, dopo di che la nonna invita di nuovo i nipoti a rispondere, così due dicono: "Io ce l'ho rosso" ed indovinano. Poi passano ancora alcuni minuti e gli altri due: "Io ce l'ho bianco" ed anche loro indovinano. Come hanno fatto? N.B. I nipoti non possono assolutamente né usare specchi né alcun altro strumento e non possono nemmeno comunicare fra loro dicendo ognuno il colore del cappello dell'altro!
28	8 per mille	Si hanno a disposizione otto 8 e si deve ottenere 1000. Le regole sono le seguenti: 1) gli 8 vanno utilizzati tutti e non si possono utilizzare altri numeri se non quelli ottenuti operando sugli otto 8 iniziali. 2) si possono usare con le varie operazioni algebriche (somma, sottrazione, moltiplicazione, divisione), ma non vedo perché escludere eventuali soluzioni che utilizzino potenze, radici, ecc - se possibile - purché si usino tutti gli 8 e nessun altro numero 3) posso anche accostare due 8 per ottenere 88, tre per avere 888, ecc. (bhè... non è molto matematico!)		<!--<BR>888+88+8+8+8 = 1000 <BR>(8*8*8-8)*(8+8)/8-8 <BR>(8+(8+8)/8)^((8+8+8)/8) <BR>8*(8*(8+8)-(8+8+8)/8) <BR>8^sqr(8+8)/sqr(8+8)-8-8-8 <BR>8!/sqr(8+8)/(8+(8+8)/8)-8 <BR>(8+(8+8)/8)*(int(ln(8))+8)*(int(arctg(8)/8) <BR>(88/8)!/8!+8+(8+8)/8 <BR>8888/8.888 <BR>8!!+8!!+8!!!+8!!!!+8!!!!+8!!!!+8!!!!+8!!!!! <BR>((8+8)*8-(8+8+8)/8)*8 <BR>http://mathworld.wolfram.com/Multifactorial.html-->
29	IL PARADOSSO DI ACHILLE E LA TARTARUGA	Achille piè veloce sfida alla corsa una lenta tartaruga, dicendole: - Scommettiamo che riesco a batterti nella corsa anche se ti dò dieci metri di vantaggio? la tartaruga risponde: - Sai, io sono molto lenta, è il mio stile di vita, ma se mi dai dieci metri di vantaggio, non puoi battermi! - Sì che posso, io sono il doppio più veloce di te. - Anche se sei il doppio più veloce non potrai mai raggiungermi. Vedi, mentre tu percorri i dieci metri che io ho di vantaggio io mi sposto in avanti di cinque. Tu dovrai poi percorrere questi cinque metri, ma io mi sarò spostata in avanti di altri due metri e mezzo che tu dovrai recuperare. Ma mentre tu cercherai di raggiungermi facendo questi due metri e mezzo io mi sarò spostata di un altro metro e venticinque e così via fino all'infinito, così tu non potrai mai raggiungermi. Così dicendo la tartaruga tracciò sulla terra un diagramma che spiegava la situazione. Achille osservò a lungo il diagramma, ripetendo mentalmente più volte il percorso della gara, non riuscendo a capacitarsi di come fosse possibile che egli non riuscisse mai a raggiungere il più lento animale. D'altronde Achille poteva, ragionando in altro modo, sostenere di poter vincere la gara. Infatti quando Achille avesse percorso, diciamo, trenta metri, la Tartaruga ne avrebbe percorsi solo quindici; detratti i dieci metri di vantaggio iniziali, Achille si sarebbe ancora trovato in vantaggio di cinque metri. Il paradosso appassionò molto gli antichi, che non conoscevano la teoria delle serie e trovavano inspiegabile il ragionamento.
30	LA FRECCIA DI ZENONE	Una freccia, lanciata su un bersaglio, percorre dapprima la metà della sua traiettoria, poi la metà della metà rimanente, e così di seguito. Dividendo la traiettoria un numero infinito di volte, potrà la freccia raggiungere la sua meta?		Sembra di no perché resta sempre una metà di spazio da percorrere... e, tuttavia, la freccia raggiunge la sua meta. Questo sofisma, dovuto al filosofo greco Zenone di Elea, ha esercitato la sagacia dei più grandi pensatori dell’antichità. È il risultato del fatto che Zenone era incapace di concepire come una successione infinita di operazioni potesse corrispondere a un risultato globale finito. Inoltre, questa inettitudine dialettica era rinforzata da un partito preso metafisico: per rivalità di scuole, Zenone pretendeva di negare, contro Pitagora, la possibilità di ogni molteplicità, e, contro Eraclito, quella di ogni movimento.
31	UNA GARA FAMOSA	Il filosofo greco Zenone (V secolo a.C.) esponeva il seguente paradosso. Se il velocissimo Achille fa una gara di corsa con una tartaruga, concedendo a questa un vantaggio, anche piccolissimo, egli non riuscirà mai a raggiungerla. Infatti, diceva Zenone, supponiamo che la velocità di Achille sia 10 volte quella della tartaruga e che Achille dia alla sua rivale un vantaggio iniziale di 10 metri. All'inizio della gara Achille si trova, poniamo, in A e la tartaruga in B (e quindi la distanza AB è di 10 metri). Quando Achille avrà percorso 10 metri, e sarà quindi arrivato in B la tartaruga avrà percorso 1 m e sarà arrivata in C quando Achille avrà percorso un metro, la tartaruga avrà percorso 1/10 di metro e sarà arrivata in D: quando Achille avrà percorso anche questo decimo di metro, e sarà arrivato in D, la tartaruga avrà percorso ancora 1/100 di metro e sarà arrivata in E. E così via all'infinito. Il vantaggio della tartaruga diventerà sempre più piccolo, ma non diventerà mai zero e quindi Achille non potrà mai raggiungere e poi superare la tartaruga.
32	L'ACQUARIO MEZZO VUOTO O MEZZO PIENO	Un acquario pieno d'acqua fino al bordo pesa 108 kg. Quando è metà vuoto, lo stesso acquario pesa 57 kg. Quanto pesa l'acquario vuoto?		posto che l'acquario metà pieno pesa 57 kg, diremo che tale peso è dato da X=acqua contenuta + y=peso dell'acquario vuoto. da cui x+y=57  risolvendo per y diremo y=57-x;  l'acquario pieno è quindi (due parti di acqua + il vuoto) e cioè: 2x+y=108 che possiamo anche scrivere (sostituendo a y il suo valore espresso come x )-riduciamo in tal modo il problema ad una sola incognita-   2x+57-x=108, quindi risolvendo per x scriveremo 2x-x=108-57  ->  x=51   e finalmente  Y=57-51  =6 Ho voluto scrivere questa dimostrazione perchè so che la matematica è mal digerita da molti, ma come si può facilmente intuire da quanto sopra (equazione a due incognite) non è affatto difficile.
33	DOV'È L'ERRORE?	Se Scriviamo a^2-a^2=a(a - a) = (a + a)(a - a) Dividiamo entrambi i membri per (a - a) e otteniamo a = 2a Dividiamo ancora per a 1 = 2 Dov'è l'errore?
34	PENSA UN NUMERO	Pensa un numero moltiplicalo per 3; sottrai 2; moltiplica per 5; aggiungi 10; dividi per il numero pensato. Il quoziente che hai ottenuto è esatto ed è uguale a 15; vero?
35	UN GEOMETRA	Un geometra chiama un suo allievo gli da un block notes, una penna, un metro e gli dice di andare a rilevare le misure di una vecchia Torre poco lontano da lì. Il giovane allievo, animato da entusiasmo per il compito affidatogli, si mette subito in marcia. Arrivato nel luogo indicatogli dal suo capo si trova davanti una torre altissima situata in una zona desolata, senza alcuna casa o albero attorno. Mentre si appresta ad effettuare le misure si accorge che non c'è alcun accesso per salire sulla torre e il materiale di cui dispone (un piccolo metro) non gli consente di effettuare una misura esatta data l'enorme altezza della costruzione. Così si guarda un attimo attorno, pensa un attimo, effettua le misure e ritorna dal suo capo che gli fa i complimenti. Come ha fatto il giovane a misurare l'altezza della torre?
36	DALLA CHIROMANTE	Un signore va dalla chiromante e le chiede quanti anni sarebbe vissuto. La chiromante, dopo avere attentamente esaminato la mano del cliente, gli dice: "Lei raggiungerà l'età di suo nonno, più tre quarti dell'età stessa, meno quattro quinti dell'età raggiunta da sua nonna, la quale visse esattamente 13 anni in meno di suo nonno." L'interessato fa i conti e trova, fortunato lui, che vivrà fino a 94 anni. Sapendo questo, dite le età raggiunte dal nonno e dalla nonna.
37	TRE AMICI, TRE PASSIONI, QUANTI ANNI?	Tre ragazzi, di età abbastanza vicini tra loro, 22, 24, 25 anni, rispettivamente, sono di aspetto piuttosto diverso e hanno anche passioni diverse ma sono molto amici. Il tennista sfegatato, ha i baffi, mentre quello la cui età è divisibile per 5 è biondo e quello appassionato di pallavolo è contento che la sua età abbia come somma delle cifre il numero di giocatori di una squadra del suo sport preferito. Sapendo ciò, potete dire quanti anni ha l’appassionato di musica?
38	CURIOSA SPARTIZIONE	Due Arabi, l’uno recante 5 pani, l’altro 3 pani, incontrano in campagna un viaggiatore ricco e affamato. Fanno colazione insieme, poi il viaggiatore, come prezzo del suo pasto, dà loro 8 monete d’oro. Come fare la spartizione?		Il primo Arabo, quello che possedeva 5 pani, giudica che gli spettino 5 monete, lasciando le altre 3 al compagno. Questi replica che gli spettano 4 monete e che rimborserà al primo il prezzo di un pane. In conclusione, l’accordo non può essere raggiunto. Il cadì, consultato, risolve così la vertenza: Avete torto tutti e due, dice. Si può supporre che abbiate diviso ciascuno dei vostri pani in 3 parti uguali, ciò che fa in tutto 24 parti, di cui ciascuno di voi ne ha mangiate 8. Quello che aveva 5 pani o 15 parti ha ceduto 15 — 8 = 7 delle sue parti al viaggiatore; quello che aveva 3 pani o 9 parti gli ha ceduto solamente 9 — 8 = 1 parte. Spettano dunque 7 monete d’oro a quello di voi che possedeva 5 pani e una sola moneta all’altro.
39	IL TESTAMENTO DELL’ARABO	Un Arabo muore lasciando per testamento ai suoi tre figli la sua fortuna composta di 17 cammelli; ne lascia la metà al maggiore, la terza parte al secondogenito e la nona parte al più giovane. Si domanda come i tre figli abbiano effettuato la divisione dei cammelli.		al maggiore:9 cammelli al secondo: 6 cammelli al terzo: 2 cammelli
40	L'ASINO E IL MULO	Un asino diceva un giorno ad un mulo: se prendessi 20 Kg del tuo carico il peso che mi opprime diventerebbe doppio del tuo. Il mulo lo rispose: se io prendessi 20 Kg del tuo peso, io porterei un carico uguale al tuo. Quale peso portava ciascun animale?
41	IL BARCAIOLO	Un barcaiolo è in mezzo ad un lago sulla sua barca. Ha con sé un grosso macigno. Se lo getta nel lago, cosa accadrà al livello dell'acqua ai bordi della costa?
42	BATTAGLIA DEI NUMERI: UN GIOCO A DUE ASSAI NOTO, CON REGOLE SEMPLICI	Il gioco si svolge così: uno dei due giocatori sceglie un numero da 1 ad n (con n numero naturale qualunque). L'altro aggiunge al numero scelto dall'avversario un altro numero compreso sempre fra 1 ad n. Si continua così addizionando alternativamente alla somma precedentemente raggiunta un numero compreso fra 1 ed n. Vince chi raggiunge per primo la somma di 100. Strategia vincente è la seguente: 1) se n + 1 non è divisore di 100, il primo giocatore si assicura la vittoria scegliendo al primo turno il resto della divisione di 100 per n + 1 e ai turni successivi tutti gli altri numeri che si ottengono a partire da questo resto aggiungendo sempre n + 1; 2) se n + 1 è divisore di 100, allora è il secondo giocatore ad assicurarsi la vittoria raggiungendo al primo turno n + 1 e quindi tutti gli altri numeri che si ottengono a partire da questo sommando sempre n + 1.
43	I QUADRATI E I RETTANGOLI DELLA SCACCHIERA	Quanti quadrati e quanti altri rettangoli ci sono in una scacchiera? O meglio, in quanti modi è possibile tracciare un quadrato o un altro rettangolo limitati dalle linee dei quadrati unitari della scacchiera? Si devono contare, oltre agli 8x8 = 64 quadrati unitari anche quelli 2x2, 3x3 e tutti quelli più grandi. Alla fine si arriva ad una formula che si può applicare a scacchiere di dimensioni diverse. Ad esempio, quanti sono i quadrati per una scacchiera 10x10?	di H. E. Dudeney (1857 - 1930), grande esperto inglese di giochi matematici	Questa frase e' falsa
44	GLI ZERO TRA UNO E UN MILIONE	Quanti zero sono necessari per scrivere tutti i numeri da 1 a un milione?		Siamo riusciti quindi a ottenere una formula ricorsiva per calcolare quanti "zero" occorrono per scrivere tutti i numeri di n + 1 cifre: Zn+1 = (9 . 10^(n-1) + Zn) + 9 . Zn = 9 . 10^(n-1) + 10 . zn 1 milione: 488895
45	3 cifre	Quanti sono i numeri di tre cifre la cui somma delle stesse tre cifre sia uguale a 9?
46	CIFRE DISPARI	Sapendo che A,B,C sono cifre dispari, calcolarne i valori e il risultato della seguente operazione: AB/C =? in modo che il risultato sia sempre uno ed uno solo e che sia il più lontano possibile da AB. 7 Se 84 = 8x8x8x8 8³= 8x8x8 8²= 8x8 8¹= 8 80,5 =? N.B. In questo gioco non c'è molto di matematico, usa la fantasia! P.S. Non c'entra la radice quadrata
47	IL PIÙ GRANDE NUMERO FORMATO CON TRE CIFRE	Qual è il più grande numero che si possa scrivere con tre cifre?		9 portato alla potenza 9 e il risultato portato anch’esso alla potenza 9. È un numero imponente perché comprende circa 369 milioni di cifre significative, e accordando, per scriverlo, 4 millimetri a ciascuna di esse, misurerebbe: 1.478 km, 772 m, 40 cm
48	LE CIFRE	Quante cifre ha il numero (123456789)^6?
49	NUMERI E MULTIPLI	Siano dati 864 numeri, anche non consecutivi. Esistono due numeri x e y fra questi tali che x-y sia multiplo di 653? Si tratti lo stesso problema quando siano dati 653 numeri: esistono x e y fra questi tali che x-y è multiplo di 864? Si discuta il caso di due numeri m ed n qualsiasi.
50	PRODOTTI SINGOLARI	12345679x9=111111111 12345679x8=98765432 1x9+2=11 12x9+3=111 123x9+4=1111 1234x9+5=11111 12345x9+6=111111 123456x9+7=1111111 1234567x9+8=11111111 12345678x9+9=111111111 9x9+7=88 98x9+6=888 987x9+5=8888 9876x9+4=88888 98765x9+3=888888 987654x9+2=8888888 9876543x9+1 =88888888 98765432x9+0=888888888 1x8+1=9 12x8+2=98 123x8+3=987 1234x8+4=9876 12345x8+5=98765 123456x8+6=987654 1234567x8+7=9876543 12345678x8+8=98765432 123456789x8+9=987654321
51	PRODOTTO TRA TUTTE LE LETTERE	Quanto fa (x-a)(x-b)(x-c)(x-d)...(x-z)?		Suggerimento: controlla il 24-esimo fattore.
52	QUATTRO 5 PER 55	Inserire fra i quattro 5 l'opportuno segno di operazione e aggiungere, se necessario, delle parentesi in modo che sia verificata la seguente uguaglianza: 5... 5... 5... 5 = 55
53	UN CALCOLO CURIOSO	Moltiplicazione di quattro numeri interi consecutivi. Moltiplichiamo 4 numeri interi consecutivi a partire da 1: 1 x 2 x 3 x 4=24 aggiungiamo 1: 24 + 1=25 osserviamo che si ottiene un quadrato: Ora moltiplichiamo 4 numeri interi consecutivi a partire da 2: 2 x 3 x 4 x 5=120 aggiungiamo 1: 120 + 1 =121. Osserviamo che anche questo è un quadrato: Moltiplichiamo 4 numeri interi consecutivi a partire da 3: 3 x 4 x 5 x 6 = 360 aggiungiamo 1: 360 + 1 =361. Anche questo è un quadrato: Come mai?
54	Calcolo cusioso	Prendi una calcolatrice e scrivi 1111111, poi 11111*11111, quindi 111111111*111111111. Cosa viene? Sai spiegare il perché? Ora scrivi 123*8 + 3, poi 12345*8 + 5, poi 123456789*8 + 9. Cosa viene? Adesso scrivi il numero 142857, e moltiplicalo per 2. Cosa viene? E se lo avessi moltiplicato per 3, 4, 5, o 6?
55	Indovina il numero	Pensa ad un numero qualsiasi. Aggiungi ad esso il voto che hai in matematica. Ora scrivi il numero, ed anche il suo contrario aumentato di 9 (ad esempio, se fosse 187, scrivi anche 781 + 9 = 790). Sottrai il minore dal maggiore. Ora somma le cifre del risultato, anche più volte, finché non ne ottieni solo una. Questo è il tuo nuovo voto di matematica se sai spiegare perché poteva venire solo quel numero!
56	IN AUTOSTRADA	Percorrendo un tratto autostradale alla velocità costante di 120 km/h, un automobilista sorpassa, in 30 minuti, 50 camion che a loro volta marciano a una velocità di 80 km/h. Ora, supponendo costanti tutte le velocità in gioco e soprattutto mantenendo costanti i flussi di traffico, quanti camion percorrono quell'autostrada in un'ora? In poche parole un'ipotetica persona ferma al lato della strada quanti camion vedrebbe passare davanti a sé in un'ora?
57	IL CANE E LA LEPRE	Al limite di un campo lungo 150 piedi si trova un cane e sul lato opposto si trova una lepre. Il cane parte all'inseguimento della lepre quando questa inizia a correre. Mentre il cane in un salto fa 9 piedi la lepre ne fa 7. Dica, chi vuole, quanti piedi e quanti salti fecero il cane inseguendo e la lepre fuggendo, prima di essere raggiunta	Un problema di Alcuino di York, ripreso dal suo libro di problemi matematici divertenti, ad uso dei giovani studenti, Propositiones ad acuendos Juvenes, riprendendo un testo più antico del Venerabile Beda. È la Propositione XXVI. Dicat qui velit - scrive Alcuino - quot pedes quotque saltus canis perseguendo, e lepus fugiendo, quoadusque comprehensus est, fecerunt.
58	IL NUMERO DEI CAPELLI	Provare che esistono in Italia almeno due persone che hanno il medesimo numero di capelli.		Ammettiamo che una persona possa avere al massimo 100.000 capelli e al minimo 1. Non si potranno trovare che 100.000 persone al massimo che abbiano un numero differente di capelli, che abbiano dunque rispettivamente un numero di capelli espresso dai numeri interi successivi da i a 100.000. Ora, l’Italia supera i 50 milioni di abitanti. Esistono dunque, almeno, due persone che hanno il medesimo numero di capelli
59	1,2 o3?	Il cappellaio Matto, mentre si versa una tazza di tè, dice ad Alice: Io ho pensato a un numero compreso tra 1 e 3. Tu ora devi scoprire di quale numero si tratta, avendo la possibilità di pormi un'unica domanda, alla quale io potrò rispondere soltanto "Sì", "No" o "non lo so", senza dover svolgere alcuna operazione aritmetica.		Io ho pensato un numero compreso tra 2 e 3, è maggiore del tuo?
60	MATEMATICI RIBELLI	Dopo una retata di matematici ribelli, rei di aver tramato contro il Re, dieci di loro, i capi del complotto, vengono condannati a morte; ma il Re, appassionato di problemi matematici, propone loro una sfida: "Dopo che vi sarete messi in fila, uno davanti all'altro, dal più alto al più basso, in modo che ognuno di voi possa vedere le persone che ha davanti a sé, farò mettere sul vostro capo un cappello bianco o nero, partendo dal primo della fila, quello più alto. Voi non potete girarvi indietro e non conoscete quindi il colore del cappello che avete in testa, né quello delle persone che sono dietro di voi. Sempre partendo dal primo della fila (quello che ha nove cappelli davanti a sé) dovrete poi dirmi il colore del vostro cappello e io grazierò tutti quelli che avranno indovinato. Dovrete quindi rispondere soltanto "bianco" o "nero". Chi bara o chi si volta indietro verrà immediatamente giustiziato". I condannati avevano già sentito parlare di questo rituale dei cappelli al quale erano stati sottoposti altri condannati prima di loro, e così prima di presentarsi davanti al Re avevano avuto tutto il tempo per accordarsi, in modo da salvare la vita al maggior numero di persone. Qual è la strategia migliore?
61	TRE MATEMATICI RIBELLI	3 Matematici ribelli che avevano tramato contro la monarchia, vengono catturati e condannati a morte. Ma il re decide di offrire loro una possibilità di salvezza. "So che siete ottimi matematici - dice il re - e quindi logici raffinati. Intendo sottoporvi a una prova e chi di voi la supererà, avrà salva la vita. Vedete questi cappelli, tre bianchi e due neri? Ora metterò sulla testa di ognuno di voi uno di questi cappelli e nasconderò i due rimasti. Voi potete vedere i cappelli in testa ai vostri compagni, ma non vedete quello che voi stessi avete in testa. Naturalmente non potete comunicare fra voi, ma dovrete dirmi soltanto il colore del vostro cappello, spiegandomi i motivi della vostra scelta, in modo che questa non sia soltanto casuale. Chi mi darà una spiegazione convincente avrà salva la vita". Il re mette poi sulla testa dei prigionieri i tre cappelli bianchi e nasconde i due neri. Il primo matematico guarda i cappelli dei compagni e sconsolato confessa: "Non so rispondere". Anche il secondo matematico ammette di non saper rispondere. Il terzo matematico, dopo un attimo di riflessione risponde: "Il mio cappello è bianco!" Qual è stato il suo ragionamento?
62	UN CARCERATO	Un carcerato con l'aiuto di un complice libero, studia un piano per evadere dal carcere. Egli è rinchiuso in una cella a pian terreno con una piccola grata che si affaccia all'esterno. Così dice al complice di presentarsi una notte con una macchina ed una corda abbastanza robusta in modo da legarla alle sbarre della grata e con la macchina tirarla affinché si divelta. Al momento dell'evasione, però, il carcerato si accorge che la corda portata dal complice non è adatta allo scopo. Essa, infatti, è spessa 3 cm, lunga 6 m e presenta alle due estremità due rigonfiamenti, che acquistano uno spessore di più di 10cm. Le sbarre della grata, invece, distano l'una dall'altra solo 8 cm, quindi il capo della corda non può passare assolutamente fra le sbarre e non è possibile perciò legare la corda in questo modo. Dopo alcuni secondi però l'astuto carcerato riesce a farlo senza apportare alcuna modifica alla corda ed è finalmente libero. Come ha fatto?
63	LA PARTITA A CARTE	Antonio, Beppe e Carlo hanno organizzato una sfida a carte; ogni partita ha avuto un solo vincitore. 1 - Il giocatore che per primo si è aggiudicato tre mani è stato dichiarato vincitore della sfida. 2 - Nessun giocatore ha vinto due partite consecutive. 3 - Antonio è stato il primo a dare le carte, ma non l'ultimo. 4 - Beppe è stato il secondo mazziere. 5 - I giocatori sedevano in posizioni fisse attorno al tavolo: il giocatore alla sinistra del mazziere corrente dava le carte nella mano successiva. 6 - Quando un giocatore è stato di mazzo, in quella mano non ha mai vinto. Chi ha vinto la sfida?
64	QUANTE CASTAGNE TOCCARONO A OGNI BAMBINA?	Tre bambine, Mary, Nelle e Susie, raccolgono 770 castagne e se le spartiscono in modo che i numeri delle castagne toccate a ciascuna siano nella stessa proporzione delle rispettive età. Per ogni quattro castagne prese da Mary, Nellie ne prese tre, e per ogni sei castagne prese da Mary, Susie ne prese sette. Quante castagne toccarono a ciascuna?	Un problema del grande enigmista Sam Loyd
65	LA CATENA D'ORO	Un tale possiede una catena d'oro composta da sette anelli e non richiusa su se stessa. Un giorno, spinto dal bisogno, è costretto a chiedere in prestito un cavallo ad un suo conoscente per sette giorni. In cambio però, quest'ultimo vuole la catena d'oro e chiede di venir ricompensato con un anello al giorno, per ognuno dei sette giorni. Qual è il numero minimo di anelli della catena che occorre rompere perché questo sia possibile? E se invece la catena fosse composta di 30 anelli e gli scambi avvenissero in 30 giorni?
66	IL CIOCCOLATO CON IL BUONO PREMIO	Una nota azienda di cioccolato ha messo in commercio tavolette di cioccolato che in ogni confezione hanno un buono premio. Dieci di questi buoni danno diritto a un'altra tavoletta di cioccolato. Qual è il valore effettivo di una di queste tavolette di cioccolato, incluso il buono premio?
67	LE RAGAZZE DEL COLLEGE	Tre ragazze di diverse nazionalità hanno i capelli di colore diverso, rossi, neri e biondi. Una è inglese, l'altra è danese e la terza è olandese. Le tre ragazze si trovano nello stesso college, in stanze vicine, ai numeri 49, 51 e 53. La ragazza con i capelli rossi è danese. La ragazza bionda è nella stanza il cui numero è divisibile per 3. La ragazza inglese è nella stanza il cui numero è un quadrato. Qual è il numero della stanza in cui si trova la ragazza olandese e qual è il colore dei suoi capelli?
68	TORNEO DI CALCIO	Nel torneo di calcio di serie A, da qualche anno, partecipano 18 squadre. Ognuna incontra le altre in una gara di andata ed una di ritorno, così che si è soliti dividere il campionato in girone di andata e girone di ritorno. Sapresti dire rapidamente quante partite vengono disputate complessivamente nel girone di andata?
69	CIN CIN!	In una tavolata di dieci persone quanti cin cin vengono fatti se ognuno lo fa con ciascun altro?
70	I DIECI CAPPELLI	Dieci amici vanno una sera al ristorante e depositano i loro cappelli al guardaroba. Se all'uscita i cappelli vengono distribuiti a caso, qual è la probabilità che nessuno di loro ritiri il proprio cappello, ma quello di un amico?.
71	OGGI IL MIO COMPLEANNO	Il prodotto della metà (in anni) per il numero dei miei figli, per il numero dei miei Cugini è 2255. Sapresti dirmi quanti anni compio? In una stanza vi sono cinque orologi: il primo va avanti 1 m ogni ora, il secondo va avanti 2 m ogni ora, il terzo ritarda 1 m ogni ora, il quarto ritarda 3 m ogni ora; il quinto, invece, fermo. Quale orologio segnerà l'ora esatta certamente una volta ogni 10 giorni, quale due volte al giorno?
72	1 EURO MANCANTE	Ci sono tre amici che si trovano una sera e decidono di andare insieme a cena in un ristorante della loro città. Alla fine della cena, chiedono naturalmente il conto al cameriere, che immediatamente porta loro un biglietto dal quale risulta che la spesa complessiva ammonta a 30 Euro. A questo punto i tre amici estraggono ognuno una banconota da 10 Euro e la porgono al cameriere, lamentandosi però perché trovano il conto piuttosto caro, e chiedono quindi al cameriere di andare dal suo capo per chiedere un piccolo sconto. Il cameriere si reca allora dal direttore riferendo quanto gli è stato detto, e quest'ultimo decide di accettare la richiesta applicando uno sconto di 5 Euro. Subito dopo il cameriere prende 5 monete da 1 Euro dalla cassa e li riporta ai tre amici, i quali decidono di riprendere 1 Euro a testa e lasciano i restanti 2 Euro al cameriere come mancia, in segno della sua disponibilità. Usciti dal locale i tre amici cominciano a fare i conti: dunque, ognuno di loro ha in pratica speso 9 Euro, per un totale di 27 Euro, più 2 Euro dati al cameriere si arriva ad una somma di 29 Euro, ma dove è finito il restante 1 Euro che manca ai 30 Euro iniziali?		L'euro non è finito da nessuna parte. Infatti il gioco è intenzionalmente posto con lo scopo di ingannare colui che deve risolverlo. La spiegazione è molto semplice: si può facilmente osservare che i 27 euro complessivamente sborsati dai tre amici, sono stati così suddivise: 25 euro al direttore del ristorante e i restanti 2 sono la mancia data al cameriere.
73	UNA CORDA E TRE ANIMALI	Immaginate di avere una corda lunga quanto la circonferenza terrestre (cioè all'incirca 40000 km), che si trova distesa lungo l'equatore. Immaginate ora di prendere questa corda, di tagliarla, di aggiungervene un metro e quindi di ridistribuirla attorno all'equatore in modo che abbia una distanza dalla superficie terrestre che rimanga costante lungo tutta la circonferenza. La domanda a cui dovete cercare di rispondere è: quale dei seguenti tre animali può passare di misura nello spazio interposto tra la corda e la superficie: una formica, un gatto o un elefante?
74	LO SPAGO INTORNO ALL’EQUATORE	Uno spago circonda esattamente l’equatore. Esso viene tagliato in un punto e vi si aggiunge un pezzo di spago lungo 1 metro. A quale distanza dall’equatore si potrà allora collocarlo?		Abitualmente, si ritiene è che questa distanza sia estremamente piccola e che sia dell’ordine del milionesimo di millimetro o meno ancora. In realtà, il calcolo mostra che è uguale à 15 cm circa
75	LA CORNICE	Con questa cornice - dice il negoziante -il quadro costa € 8.75 e con quest'altra, più bella e che costa il doppio, il prezzo è di €10. Quanto costa il quadro senza cornice?
76	CUNEGONDA, SANTA DI PROFESSIONE E MATEMATICA PER DILETTO	Un poveretto aveva pochi soldi. Allora pregò Santa Cunegonda che gli raddoppiasse i denari in cambio egli avrebbe donato 8000 lire ai poveri. Santa Cunegonda esaudì i suoi desideri ed egli diede 8000 lire ai poveri. Visto che la cosa funzionava, il poveretto ripregò Santa Cunegonda che gli raddoppiasse i denari: in cambio egli avrebbe donato ancora 8000 lire ai poveri. Santa Cunegonda lo esaudì ed egli mantenne la parola. Non contento, si rivolse di nuovo a Santa Cunegonda per farsi raddoppiare i denari; in cambio avrebbe donato altre 8000 lire ai poveri. Santa Cunegonda lo esaudì ancora ed egli donò 8000 lire ai poveri. Ma, in questo modo, il poveretto si ritrovò senza una lira. Quanti soldi aveva all'inizio?
77	LE FACCE DI UN DADO	In quanti modi possiamo segnare le facce di un dado affinché 1 e 6, 2 e 5, 3 e 4 siano su facce opposte?
78	SOMMA DI TRE DADI	Prendete tre dadi e fate questo giochetto a un amico. Ditegli di lanciare i dadi mentre gli voltate la schiena e di addizionare i valori apparsi sulle facce. Fategli quindi scegliere un dado e ditegli di addizionare al totale precedente il numero che compare sulla faccia inferiore del dado stesso. Questo è gettato di nuovo, e il valore che ora appare viene aggiunto al totale precedente. A questo punto giratevi, e fate notare che non potete sapere che dado è stato scelto e tratto la seconda volta, ma che potete dire ugualmente quale sia il totale di tutti i valori sommati. Basterà, semplicemente, aggiungere 7 al valore della somma dei numeri che compaiono sulle facce superiori dei tre dadi. Questo giochetto si spiega facilmente con l'algebra. Lanciamo tre dadi: a, b, c, rappresentino i valori apparsi sui dadi stessi. Addizioniamo i numeri apparsi sulle facce: a + b + c. Scegliamo un dado e aggiungiamo alla somma precedente il numero che compare sulla faccia inferiore. Osservando che le facce opposte di un dado danno sempre come somma 7, il numero sulla faccia opposta ad a sarà 7-a, su quella opposta a b sarà 7—b, e su quella opposta a c sarà 7—c. Se a è il numero che compare sul dado scelto, la nuova somma sarà (a+ b + c) + (7 — a) = b + c+ 7. Poiché tutti e tre i dadi hanno la stessa caratteristica disposizione dei numeri, la nuova somma sarà sempre uguale a 7 aumentato dei valori che compaiono sui due dadi non scelti. Lanciando di nuovo il dado si ottiene un altro numero da addizionare, supponiamo d, e la somma è b+c+7+d. Ciò che vedete sulla tavola è b + c + d. Ciò che il vostro amico ha totalizzato b+c+d+7. Quindi non vi resta che addizionare 7 ai valori che compaiono sui tre dadi per avere il totale ottenuto dall'amico.	Da: Johnson—Glenn Divertimenti matematici, Zanichelli
79	PAGARE IL DAZIO	Il problema che segue è di W. Rouse Ball, celebre esperto inglese in giochi matematici, del secolo scorso: Due commercianti di vini arrivano a Parigi, uno con 64 botti e l'altro con 20 botti, tutte dello stesso valore. Ma non avendo sufficiente denaro per pagare il dazio, il primo paga 40 franchi con in più 5 botti. Il secondo lascia due botti e gli vengono restituiti 40 franchi. Qual è il prezzo di una botte e del dazio corrispondente?
80	UNA UGUAGLIANZA PARADOSSALE	Dimostrare che: 2=1. Si ha evidentemente: 0=0 Cioè 2—2=1—1 Oppure: 2x(1—1)=1—1 Dividendo i due membri dell’uguaglianza per (1—1), si ottiene: 2=1. Dov'è l'errore?		Non si può dividere per zero
81	I DISCEPOLI DI PITAGORA	Si racconta che un giorno Policrate, il tiranno di Samo, chiese a Pitagora quanti fossero i suoi discepoli. "La metà - rispose Pitagora - studia le belle scienze matematiche; l'eterna natura è l'oggetto dei lavori di un quarto; un settimo si esercita nel silenzio e nella meditazione; ci sono infine tre donne fra le quali la migliore è Teano [moglie di Pitagora]. Ecco, o Policrate, il numero dei miei discepoli che lo sono anche delle Muse". Quanti erano i discepoli di Pitagora?
82	TRE UOMINI IN FUGA	Suona l'allarme nel carcere di Rebibbia: al momento del rientro dei detenuti nelle celle, dopo l'ora d'aria, le guardie carcerarie hanno scoperto che tre pericolosi rapinatori sono evasi. Interviene immediatamente la polizia organizzando l'inseguimento dei fuggitivi nei dintorni e sguinzagliando Rex, veloce e abile pastore tedesco, che subito si getta sulle tracce dei fuggiaschi. Gli evasi hanno mezz'ora di vantaggio sui loro inseguitori, ma indeboliti dalla lunga detenzione procedono penosamente a 4 km/ora; i poliziotti, giovani e allenati, coprono senza sforzo 6 km/ora, mentre il cane corre a 12 km/ora. Rex raggiunge gli evasi e immediatamente si volta e torna dai suoi padroni; quando li ritrova, si volta di nuovo e riprende a inseguire i fuggitivi, effettuando quindi una serie di corse e di dietro-front, finché i poliziotti raggiungono e catturano gli evasi. Quanti chilometri ha percorso Rex a questo punto?
83	IL VECCHIO DISCO	Un vecchio disco di musica leggera, a 45 giri, è inciso nella zona compresa tra i diametri di 17 e 11 cm. e la sua audizione richiede esattamente 2 minuti e 30 secondi. Quanto è lungo il percorso che la puntina compie dall'inizio alla fine del disco?
84	DUE TRENI PER (UNA) MOSCA	Due treni partono contemporaneamente, uno dalla stazione di Milano diretto a Bologna e l'altro dalla stazione di Bologna diretto a Milano. Questi due treni non effettuano fermate intermedie e si può supporre che entrambi si muovano con una velocità costante di 100 km/h. Nello stesso istante in cui i due treni partono, una mosca che si era posata sulla locomotiva del treno di Milano, spaventata dal movimento, prende il volo e comincia a percorrere i binari che portano a Bologna, con una velocità di 120 km/h. La mosca, terrorizzata ed intontita, continua il suo cammino lungo i binari, fino ad incontrare il treno partito da Bologna. A questo punto, la mosca, presa dal panico, inverte la rotta e si dirige di nuovo verso Milano, sempre con la stessa velocità. In seguito, quindi, la mosca continua il suo viaggio, invertendo la sua direzione ogni volta che incontra uno dei due treni. A causa di un errore sugli scambi ferroviari, i due treni sono destinati a scontrarsi frontalmente (di questi tempi non è neppure così insolito), e di conseguenza per la povera mosca si prospetta una brutta fine. Supponendo, con una piccola approssimazione, che la distanza Milano - Bologna sia esattamente di 200 km, qual è lo spazio totale percorso dalla mosca prima di rimanere schiacciata tra i due treni?		Per il 30) Il punto è il calcolo del tempo che impiegheranno i due treni a scontarsi. Sato che viaggiano alla stessa velocità e partono contemporaneamente esattamente a metà strada si scontreranno cioè dopo 100km. Per fare 100 Km ci hanno messo t=S/v=100/100=1 ora Ed è proprio 1 ora il tempo di volo della mosca perchè parte insieme, e quinsi s=vt=120*1=120 km.
85	LA MOSCA E I DUE TRENI	Due treni partono da due stazioni distanti 120 Km e si dirigono, sullo stesso binario, l’uno contro l’altro; il primo viaggia a 60 Km/h, il secondo a 40 Km/h. Da una delle due stazioni, contemporaneamente e seguendo il medesimo binario, parte anche una mosca; questa, viaggiando a 100 Km/h, incontrerà il treno proveniente nel verso opposto prima dell’altro treno. Ipotizziamo che, a questo punto, la mosca rimbalzi andando incontro all’altro treno e che scontratasi con quest’ultimo, rimbalzi ancora verso il primo treno e così via fino a rimanere schiacciata tra i due treni nel momento dello scontro. Quanti Km avrà fatto la mosca prima di rimanere schiacciata ?
86	ANDATA E RITORNO	Il signor Verdi deve intraprendere un viaggio da Milano a Torino. Per non rientrare a casa troppo tardi, decide che dovrà compiere l'intero tragitto (andata e ritorno) a una velocità media di 60 km/ora. Arrivato a Torino si rende conto però di avere tenuto una media di 30 km/ora. Quale deve essere la velocità media del signor Verdi nel viaggio di ritorno, per alzare la media dell'intero percorso ai 60 km/ora come stabilito inizialmente?
87	IL CICLISTA E IL MOTOCICLISTA	Un ciclista parte alle 5 del mattino e fa, in media, 20 km all'ora. Alle 9 parte un motociclista il quale deve raggiungere il ciclista in due ore. Quanti km all'ora dovrà percorrere il motociclista?
88	UN MAGNIFICO SALICE	È piantato all'interno di un terreno quadrato. La somma delle sue distanze da due lati del quadrato è di 100 m, mentre la somma delle distanze dagli altri due lati è uguale a 120 m. Qual è l'area (in metri quadrati) del terreno?
89	DOMANDINE QUASI INTELLIGENTI	• LA STANZA - Entri in una stanza completamente buia con un cerino ed hai una candela ed una lampada ad olio. Cosa accendi per prima? • I MESI - Quanti mesi arrivano a 28 giorni? • IL CACCIATORE - Su un filo elettrico sono disposti in fila 22 uccelli. Un cacciatore ne uccide 9 e 13 volano via. Quanti restano vivi? • L'ARCA - Quanti animali portò Mosè sull'arca? • LA LUMACA - Una lumaca deve salire un muro di 3 metri. Di giorno sale di 2 metri, ma di notte ne scende di 1.Dopo quanti giorni arriva in cima al muro? • IL METRONOTTE - Un metronotte viene ucciso di giorno. Ha diritto alla pensione? • GIUSEPPE - Il padre di Giuseppe ha tre figli: Qui, Quo e...........? • IL DISASTRO AEREO - Un aereo cade sul confine tra l'Italia e la Svizzera. Dove saranno sepolti i superstiti? • IL NUMISMATICO - Un numismatico dice di possedere una moneta antica con la dicitura 42 a.C. È vero o falso? • IL MATTONE - Un mattone pesa un chilo più mezzo mattone. Quanto pesa un mattone? •  UN MILIONE - Ti accontenteresti di vivere solo un milione di ore? • LE MANI - Rispondi rapidamente! Quante dita ha una mano? E due mani? E dieci mani? • RISPONDI IMMEDIATAMENTE - Pesa di più un chilo di ferro o un chilo di paglia? •  POCO - Qual è la differenza fra il più piccolo numero di sei cifre e il più grande numero di cinque cifre?
90	UN ELASTICO	Un elastico lungo tre metri è fissato da una parte. Una formica si muove lungo l’elastico percorrendo un metro al minuto. Dopo un minuto l’elastico, partendo da un’estremità, si allunga di altri 3 metri. Questo si ripete alla fine di ogni minuto, finché la formica non raggiunge l’estremità dell’elastico. Assumendo che l’elastico possa essere allungato così tanto, quanto tempo impiegherà la formica per arrivare alla fine?
91	UN ENOLOGO	Un enologo ha a disposizione una gran quantità di vino (non importa quanto, ma molto vino). Ha quattro tipi di vino che vengono sistemati in un determinato numero di damigiane. Tenendo presente che le damigiane possono contenere anche tutte lo stesso tipo di vino, si calcola che le combinazioni possibili dei 4 tipi di vino sistemate per ogni botte sono 16384. Sapendo che ogni damigiana contiene un solo tipo di vino e può contenere al massimo 10 L., quanti litri di vino vengono messi nelle damigiane affinché sia possibile il numero di combinazioni trovato? E quante devono essere le damigiane?
92	L'ETÀ	Io ho il doppio dell'età che avevi tu quando io avevo la tua età. Inoltre la somma della mia età e quella che avrò quando tu avrai la mia età è 90. Quanti anni ho io e quanti tu?	da un idea di Carmine Barra
93	LA NAVE	In mezzo al mare c'è una nave con la nota rampa di scalini che fuoriesce dal bordo della nave e tocca la superficie dell'acqua e che serve ai marinai per salire a bordo. Si osserva che la rampa è costituita da dieci scalini e che la distanza fra uno scalino e l'altro è di 10cm. Trascurando lo spessore degli scalini, calcolare quanti scalini rimangono fuori dall'acqua se si alza un'alta marea di 33cm.
94	FRAZIONE GENERATRICE	Vuoi capire il perché della regola che consente di trovare la frazione generatrice di un numero decimale periodico? Indica con x un qualunque numero decimale periodico; ad esempio 7,32444... Puoi scrivere che: x=7,32(4)=7,32+0,00(4). Se moltiplichi x per 10, ottieni: 10x=73,2(4)=73,24(4)=73,24+0,00(4). Pertanto hai: 10x—x[73,24+0,00(4)]-[7,32+0,00(4)] Tenuta presente la 1a proprietà della sottrazione, la precedente uguaglianza diviene: 9x=73,24-7,32 per cui: x=(73,24-7,32)/9=(7324—732)/900 Come vedi, hai ritrovato proprio la frazione generatrice del numero x, prevista dalla nota regola. Prova, ora, a ripetere il ragionamento precedente riferendoti ad altri numeri periodici. Ad esempio a 2(48); 0,12(7); 3,(465). Tieni presente che x va moltiplicato per 10,o per 100 o per 1000,..., a seconda che il suo periodo sia di 1, o di 2 o di 3,..., cifre.
95	FUNGHI E FUNGHETTI	Sette amici, vanno a raccogliere funghi e alla fine della giornata hanno complessivamente ben 100 funghi nei loro panieri. Ognuno degli amici ha raccolto un numero diverso di funghi: sapreste provare che ci sono tre amici che, insieme, hanno raccolto almeno 50 funghi?
96	LA GALLINA	Se una gallina e mezzo fa un uovo e mezzo in un giorno e mezzo, quante uova farà una gallina in sei giorni
97	I GATTI	In un certo anno, nacquero, a Parigi, un milione di gatti. Uno su 10 di quei felini mori in quell'anno e uno ogni 10 dei sopravvissuti morì nell'anno successivo. E così via negli anni seguenti. Quanti di quei gatti morirono entro il sesto anno? Fai i tuoi calcoli e dopo soltanto leggi quanto segue. Il calcolo si abbrevia notevolmente sé, invece di contare i gatti defunti, si contano i gatti sopravvissuti. Essi, alla fine del primo anno, erano i 9/10 di un milione; alla fine del secondo anno erano i 9/10 dei 9/10 di un milione [cioè 1.000.000x(9/10)2]. Alla fine del sesto anno essi erano 1.000.000x(9/10)6=96=813=531441. Pertanto, in quei sei anni, lasciarono questo mondo 468.559 di quei gatti.
98	SEI FIAMMIFERI	Avendo a disposizione sei fiammiferi provate a formare quattro triangoli equilateri, senza piegarli o spezzarli.		Disporre i sei fiammiferi in modo da costruire un tetraedro regolare, cioè una piramide a base triangolare, (figura tridimensionale). Molti non riescono a risolverlo perchè pensano che i fiammiferi vadano disposti su un piano
99	GLI STUZZICADENTI	Avendo a disposizione 6 stuzzicadenti tutti della stessa lunghezza, come è possibile formare 4 triangoli equilateri tutti uguali fra loro?		Disporre i sei fiammiferi in modo da costruire un tetraedro regolare, cioè una piramide a base triangolare, (figura tridimensionale). Molti non riescono a risolverlo perchè pensano che i fiammiferi vadano disposti su un piano
100	I CERCHIETTI	I cerchietti che vedete nella figura in basso sono disposti lungo una griglia ortogonale, cioè gli otto cerchietti più esterni giacciono sul perimetro di un quadrato, mentre il restante al centro del quadrato stesso. Il problema consiste nel coprire questi nove cerchietti con quattro segmenti di retta senza mai staccare la penna dal foglio. ooo ooo ooo
101	I bugiardi	"Uno è il bugiardo!" dice Pulcinella. "Due sono i bugiardi!" dice Arlecchino. "Tre sono i bugiardi!" dice Brighella. "Quattro sono i bugiardi!" dice Balanzone. "Cinque sono i bugiardi!" dice Stenterello. "Sei sono i bugiardi!" dice Gianduia. "Sette sono i bugiardi!" dice Meneghino. "Otto sono i bugiardi!" dice Rosaura. "Nove sono i bugiardi!" dice Pantalone. "Dieci sono i bugiardi!" dice Colombina. Chi dice la verità?		Pantaleone
102	IL PONTE	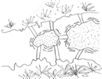Ce la fate a compiere un percorso completo, passando una volta sola su ciascuno dei sette ponti?
103	NUMERO SINGOLARE	L’illusionista scrive sulla lavagna il numero 142.857 e mostra che possiede straordinarie proprietà. Lo moltiplica per 1, 2, 3, 4, 5, 6 e fa costatare che i prodotti sono sempre espressi dalle medesime cifre che sono quelle del numero originario, e che queste cifre si permutano secondo un certo ordine: 142857•1 =142857 142857•2=285714 142857•3=428571 142857•4=571428 142857•5=714285 142857•6=857142 142857•7=999999 Tuttavia, si può osservare che la somma di queste sei cifre è 54 che è il doppio delle cifre di ciascuno dei 6 prodotti precedenti. Inoltre, questa « stanchezza » non è che passeggera, perché le cifre fatidiche non « domandano » che di riunirsi di nuovo, a condizione che le si « aiuti » un poco. Moltiplichiamo 142.857 per un numero quanto vogliamo elevato, per esempio 32.284.662.474. Il prodotto è: 4.612.090.027.048.218. In questo prodotto, non c’è più traccia del raggruppamento 142.857, ma dividiamo il prodotto ottenuto in sezioni di sei cifre a partire da destra, e addizioniamo queste sezioni; avremo: 048.218+ 090.027+ 4.612= 142.857 Talvolta, però, le cifre raggiungono con maggiore difficoltà la loro « coesione » e si deve ripetere l’addizione una seconda volta. Così, moltiplicando il numero singolare per 45.013.648, si ottiene 6430.514.712.336. Dividendo il prodotto in sezioni di sei cifre a partire da destra e addizionando, si ha: 712.336+ 430.514+ 6= 1.142.856 Separiamo ancora una volta una sezione di sei cifre, resta 1 che addizioniamo a 142.856. Si ritrova il numero singolare:142.857 Questo numero ha ancora altre curiose proprietà. Dividiamolo in due sezioni di tre cifre: 142 e 857. La seconda cifra della prima sezione, moltiplicata per il suo numero d’ordine, dà la prima cifra della seconda sezione: 4x2=8 La somma delle due prime cifre della prima sezione dà la seconda cifra della seconda sezione:1 + 4 = 5. La somma delle tre cifre della prima sezione dà la terza cifra della seconda sezione:1 + 4 + 2 = 7. Infine, se si riprendono i prodotti ottenuti moltiplicando il numero singolare per 1, 2, 3, 4, 5, 6 e li disponiamo l’uno sotto l’altro, in una tabella, si vede che la somma delle cifre di ogni sezione orizzontale e la somma delle cifre di ogni colonna verticale sono uguali alla costante 27. 1 4 2 8 5 7 = 27 2 8 5 7 1 4 = 27 4 2 8 5 7 1 = 27 5 7 1 4 2 8 = 27 7 1 4 2 8 5 = 27 8 5 7 1 4 2 = 27 27 27 27 27 27 27
104	I TRE IMBIANCHINI	Un imbianchino dipinge una stanza in 1 ora, un altro imbianchino dipinge la stessa stanza in un ora e mezzo, infine un terzo imbianchino dipinge la stessa stanza in 2 ore. Se dipingono tutti insieme la stessa stanza quanto tempo ci mettono?
105	CINQUE SOLDI DELL’EBREO ERRANTE	Se l’Ebreo errante avesse, dalla sua epoca fino alla nostra, investito 5 soldi al tasso del 5% e a interesse composto, di quale capitale disporrebbe?
106	IL PROBLEMA DEGLI INVITI	Otto persone si propongono di invitarsi reciprocamente a pranzo fino a che abbiano esaurito tutti i modi di mettersi a tavola gli uni in rapporto agli altri. Quante volte dovranno riunirsi?		8!= 40.320 giorni cioè 110 anni e 4 mesi
107	LE QUOTAZIONI DELLA GIRAFFA	Se l'ippopotamo, in una corsa, viene quotato due a uno e il rinoceronte tre a due, a quanto deve essere quotata la giraffa, se tutto viene condotto onestamente, come accade sempre nel Regno dei Giochi?	Un problema di Sam Loyd, che Martin Gardner definisce "il più grande inventore di giochi degli Stati Uniti" ( da Sam Loyd, Passatempi matematici, Sansoni, 1980)
108	L'ISOLA DEI CORNUTI	C’è un’isola, detta appunto dei cornuti, dove ai mariti traditi – ed effettivamente sull’isola ce ne sono – crescono fisicamente le corna sulla testa; e il bello è che chiunque le può vedere tranne chi le porta. Un giorno il re, per alleviare il disagio della popolazione maschile, decise di radunare tutta la popolazione in cima alla rupe più alta facendo disporre ogni uomo con la propria moglie davanti sul ciglio della rupe. E poi disse: "Farò rullare i tamburi e, al termine, chi sarà certo del tradimento della propria moglie, potrà buttarla dalla rupe per vendicarsi del tradimento". Rullarono i tamburi, ma al termine non successe nulla. Il re fece allora rullare i tamburi una seconda volta ma anche questa volta nessuno degli uomini, magari cornuti ma certo intelligenti, buttò di sotto la propria moglie. Allora il re ordinò ai tamburi di rullare ancora. Stavolta al termine si sentirono urla di terrore. Quante mogli vennero buttate giù dalla rupe?		Vennero buttate giù dalla rupe tre mogli. Dopo il primo rullo di tamburi nessuno fece nulla: quindi non c’era solo un cornuto; se infatti ce ne fosse stato solo uno, questi non vedendo nessun altro con le corna avrebbe buttato giù la propria moglie. Dopo il secondo rullo di tamburi nessuno fece nulla: quindi non c'erano solo due cornuti; infatti in questo caso ciascuno dei due, che avrebbe visto un solo cornuto, avrebbe certamente buttato giù la propria moglie avendo capito di essere lui l’altro. Dato che è dopo il terzo rullo di tamburi che successe qualcosa, vuol dire che in tre vedevano due persone con le corna. Il ragionamento è generalizzabile: il numero di mogli è uguale al numero di rulli di tamburo.
109	L'ISOLA QUADRATA	Su un’isola quadrata c’è un tesoro e bisogna raggiungerlo. L’isola è separata dalla terra ferma da un fosso molto profondo e pieno d’acqua largo 3 metri. Si hanno a disposizione solo due tavole lunghe m. 2,90 senza chiodi, corde, ecc…. Com’è possibile raggiungere l’isola?
110	IL MURO SANGUINANTE	In questo enigma devi scoprire che strade ho preso x uscire. Un giorno mi svegliai e in un labirinto mi ritrovai. Sapevo che se non ne sarei uscita avrei finito col soccombere alla Bestia immonda della catacomba. Così mi diedi da fare per cercare di capire dove andare. Ad un certo punto mi son trovata davanti ad un muro sgretolato, da esso sgorgava come bava, un liquido rosso che sembrava lava. Mi scostai ed il liquido rosso diventò un messaggio dettato da un saggio. Diceva: Usa il senno, lui ti può aiutare per uscire da questo brutto affare. Pensai...pensai e l'uscita trovai ridendo al fato che la libertà mi aveva ridato. Come ha fatto ad uscire? L'indizio che il nostro amico ci da è: "la soluzione è sotto al tuo naso"
111	LE CASSAFORTI	In un paese tutti gli abitanti sono ladri. Non si può camminare per strada con degli oggetti, senza che vengano rubati e l'unico modo per spedire qualcosa senza che venga rubato dai postini è di rinchiuderlo in una cassaforte chiusa con un lucchetto. Ovunque l'unica cosa che non viene rubata è una cassaforte chiusa con un lucchetto, mentre sia le casseforti aperte, sia i lucchetti vengono rubati. Alla nascita ogni abitante riceve una cassaforte ed un lucchetto di cui possiede l'unica copia della chiave. Ogni cassaforte può essere chiusa anche con più lucchetti ma la chiave non è cedibile e non può essere portata fuori dalla casa del proprietario, perché verrebbe rubata durante il trasporto. Non si può in alcun modo fare una copia delle chiavi. Come può un abitante di questo paese spedire il regalo di compleanno ad un proprio amico della stessa città?
112	DUE TANICHE	Avete a disposizione due taniche inizialmente vuote la cui capacità è rispettivamente di 3 e 5 litri. Avendo a disposizione tutta l'acqua che desiderate, e potendo riempire e vuotare le taniche, oltre che potere trasferire acqua da una all'altra, dovete mettere esattamente 4 litri di acqua dentro la tanica da 5. Come bisogna procedere?
113	JOHN IL LATTAIO	John era solito affermare: "Quello che non conosco in fatto di latte è così poco che non vale nemmeno la pena parlarne". Ma un bel giorno si trovò in difficoltà quando due signore gli chiesero entrambe due boccali di latte. Una di esse aveva un secchio da cinque boccali, l'altra un secchio da quattro boccali. John aveva due bidoni da dieci galloni, entrambi pieni di latte. Come fece a misurare esattamente due boccali di latte per ciascuna signora? È un semplice gioco dei bussolotti, senza trucchi né inganni, eppure ci vuole molta abilità per versare due boccali esatti di latte in ciascun secchio, facendo uso soltanto dei due secchi e dei due bidoni pieni di latte. Boccali e galloni sono unità di misura anglosassoni Un gallone corrisponde a 4 boccali e vale circa 4 litri e mezzo.	Un problema di Sam Loyd, dal suo libro Passatempi matematici, Vol. II pag. 21, Sansoni, 1980.
114	UN UOMO E LA MOGLIE	Un uomo da solo svuoterebbe una damigiana di vino in 20 giorni, se anche la moglie beve con lui, assieme svuoterebbero la damigiana in 14 giorni. In quanti giorni la moglie da sola svuoterebbe la damigiana?
115	ACQUA E VINO	Immaginate di avere davanti due caraffe, contenenti un litro d'acqua l'una, un litro di vino l'altra. Un centimetro cubo d'acqua viene passato nella caraffa del vino ed il vino e l'acqua mescolati completamente. Poi un centimetro cubo di miscela viene ripassato nell'acqua. Vi è ora più acqua nel vino che vino nell'acqua? O viceversa?	tratto da "Enigmi e giochi matematici" di Martin Gardner
116	ACQUA E VINO	Ammesso che all'inizio una caraffa contenga 10 litri di acqua e l'altra 10 litri di vino, trasferendo 3 litri avanti e indietro un numero qualsivoglia di volte e agitando dopo ogni trasferimento, è possibile raggiungere uno stato in cui la percentuale nelle due miscele sia la stessa?
117	LE BOTTI DI ACQUA E VINO	Due botti contengono rispettivamente 100 litri di acqua e 100 litri di vino. Si riempie una caraffa da 1 litro con il vino di una delle due botti e si rovescia nella botte piena d’acqua. Si riempie poi la stessa caraffa con 1 litro di acqua e vino dalla botte piena d’acqua e la si rovescia in quella piena di vino. Dopo queste due operazioni ciascuna botte contiene ancora 100 litri di liquido. A questo punto, c’è più acqua nel vino, più vino nell’acqua o le concentrazioni sono pari?
118	LE DAMIGIANE	Avete a disposizione due damigiane inizialmente vuote la cui capacità è rispettivamente di 3 e 5 litri. Avendo a disposizione tutta l'acqua che desiderate, e potendo riempire e vuotare le damigiane, oltre che potere trasferire acqua da una all'altra, dovete mettere esattamente 4 litri di acqua dentro la damigiana da 5. Come bisogna procedere? (Attenzione, bisogna usare solo queste due damigiane)
119	LA PAROLA D'ORDINE	Una spia, tentando di impossessarsi della parola d’ordine segreta che permetteva l’accesso al castello nemico, riuscì a sentire il dialogo tra la sentinella ed un soldato nemico che stava entrando nel castello: Sentinella: "12" Soldato: "6" Sentinella: "10" Soldato: "5" Sentinella: "8" Soldato: "4" Sentinella: "6" Soldato: "3" Sentinella: "OK. Passa pure." Tutto soddisfatto, convinto di aver capito tutto, si presentò a sua volta alla porta del castello; le cose andarono così: Sentinella: "12" Spia: "6" Sentinella: "10" Spia: "5" Sentinella: "8" Spia: "4" Sentinella: "6" Spia: "3" Sentinella: "4" Spia: "2" Sentinella: "Allarmi ! Allarmi ! Un nemico tenta di introdursi nel nostro castello ! " Cosa avrebbe dovuto rispondere la spia per farla franca e farsi così aprire il portone?
120	FALLIMENTO ECONOMICO	Un uomo esce dalla prigione con un fiasco di vino in mano, velocemente prosegue lungo una strada dritta finché non si trova davanti ad un albergo tutto rosso senza porte ne finestre e all'improvviso esclama: "Sono rovinato!" Cerca di darci una spiegazione che renda possibile questa situazione!
121	LA MACCHINA NERA	Una macchina nera, con i vetri neri e a luci spente sta percorrendo una strada tutta nera. In senso opposto avanza un uomo tutto nero, con cappello nero, sciarpa nera, impermeabile nero, scarpe nere... la macchina lo sta investendo quando all'ultimo momento lo evita. Come ha fatto la macchina a vederlo...?
122	LO SCAPOLONE S'È RAVVEDUTO	In un modo o nel'altro ero certissimo che si sarebbe anch'egli coniugato. Star solo all'infinito era impossibile: sono i tempi che l'hanno trasformato. Di chi si parla?
123	PROBLEMA DEI QUATTRO FERRI DI CAVALLO	Un maniscalco propone di mettere per il prezzo di 1 centesimo il primo chiodo, 2 centesimi il secondo, 4 centesimi il terzo, 8 centesimi il quarto e così di seguito fino al 32esimo chiodo, poiché ogni ferro comporta 8 chiodi. Qual è il prezzo totale della ferratura?		S= 4.294.967.295 centesimi
124	SOLDATI E ASSASSINI	In una caserma, vengono ritrovati morti tre soldati, due sicuramente assassinati ed uno con ogni probabilità suicidatosi. Il giorno seguente vengono arrestati due sospettati dell’assassinio, i quali negano il loro coinvolgimento con l’accaduto. Le indagini proseguono e giunte alla fine si scopre che i due sospettati sono innocenti per l’assassinio di uno dei due soldati uccisi. Perché si è ucciso il terzo soldato?
125	TENSIONE	Un tale entra in un corridoio, camminando arriva nei pressi di una stanza, si verifica un calo di tensione e quindi rivolta soddisfatto. Perché?
126	LA LUMACA SCALATRICE	Una lumaca è ai piedi di un albero di 15 m di altezza. Sale 2 m durante il giorno e ridiscende 1 m nel corso della notte. In capo a quanto tempo sarà in cima all’albero?		8 giorni
127	LUPI MANNARI	Una piccola città, in qualche sperduto luogo della terra, è infestata dai lupi mannari, cioè ci sono alcune persone che durante le notti di luna piena si trasformano in lupi feroci. Si può quindi ragionevolmente pensare che almeno uno degli abitanti di questo strano luogo sia un lupo mannaro. Per fare fronte a questa situazione il sindaco della cittadina emette un'ordinanza, la quale prevede che ogni cittadino che sappia di essere un lupo mannaro, si debba uccidere appena lo scopre. Dato che gli abitanti del luogo sono tutti dei cittadini rispettosi delle leggi, si può dare per certo che effettivamente ogni abitante che scopra di essere un lupo mannaro si uccida. Purtroppo però, un lupo mannaro non si accorge di esserlo e quindi lo può solo capire dall'osservazione di quello che gli sta intorno. A questo punto occorre ricordare che tutte le notti, e quindi in particolare quelle di plenilunio, ogni cittadino incontra tutti gli altri, e pertanto è in grado di vedere i lupi mannari anche se non può comunicare con loro. Dopo la terza notte di luna piena vengono ritrovati i cadaveri di alcuni lupi mannari. Voi dovete scoprire quanti sono i lupi ritrovati e soprattutto perché sono stati ritrovati soltanto dopo la terza notte, mentre nelle due precedenti non si è avuto alcun ritrovamento.		I lupi mannari morti ritrovati sono esattamente tre. Per arrivare a questa conclusione bisogna però seguire un ragionamento logico che è abbastanza semplice da capire, ma piuttosto difficile da impostare senza avere nessun ulteriore aiuto. Cominciamo col supporre che ci sia un solo lupo mannaro in città, quest'ultimo, durante la prima notte di luna piena non vede in giro nessun altro lupo, in quanto appunto egli è l'unico. Dunque, dato che è a conoscenza della presenza di almeno un lupo, capisce che l'unico lupo è egli stesso, e quindi si ucciderebbe la prima notte. Questo però non succede, quindi dobbiamo scartare l'ipotesi che ci sia un solo lupo. Supponiamo allora che i lupi siano due. La prima notte di plenilunio, ognuno di essi vede esattamente un lupo mannaro (l'altro) pensando che ce ne sia uno soltanto, e quindi, per il ragionamento fatto in precedenza, pensa che questo si ucciderà nel corso della prima notte, ma ciò ovviamente non avviene. Pertanto la successiva notte di luna piena (la seconda) i due lupi si incontrano di nuovo ed entrambi capiscono quindi che ci deve essere un secondo lupo ma dato che ne vedono solo uno, capiscono di essere anch'essi dei lupi, e si ucciderebbero nella seconda notte. Dato che la seconda notte nessuno si è ucciso, dobbiamo supporre che i lupi siano tre. Allora ognuno di questi tre, sulla base di quanto detto fin qui, penserà che gli altri due si uccideranno la seconda notte, ma la terza notte li rivede ancora e quindi capisce che ce ne deve essere un terzo, e che quel terzo deve essere lui, e quindi si uccide. Il ragionamento può essere generalizzato e possiamo quindi dire che se ci fossero n lupi, questi si ucciderebbero dopo n notti di plenilunio.
128	UN COMMERCIANTE	Un commerciante chiede ad un fabbricante d'auto di costruirgli 103 macchine. Il fabbricante però ne costruisce molte di più, perché prima di consegnarle, esattamente un terzo di esse le dà ad un altro cliente. Però, quando conta le macchine rimaste, si accorge che non bastano per soddisfare la richiesta del commerciante. Qual era il numero minimo di macchine che il fabbricante doveva costruire per non avere questo problema?
129	LE DITA DEL MARZIANO	Supponiate che un giorno riusciate a contattare un marziano e gli proponiate di risolvere una semplice equazione: x^2-16x+41=0 Se lui vi dicesse che la differenza delle radici vale 10, quante dita avrebbe il marziano?
130	LE MELE	Una vecchina con un canestro pieno di mele va bussando per le case per venderle. Alla signora della prima casa vende la metà delle mele del canestrino + mezza mela. Alla quella della seconda casa vende la metà delle mele rimaste nel canestrino + mezza mela. Infine a quella della terza casa vende la metà delle mele rimaste nel canestrino + mezza mela. A questo punto il canestro è vuoto. Quante mele c’erano nel canestro all’inizio?
131	UN AMERICANO	Un americano compra un certo numero di barche e almeno un quinto di esse le promette a suo nipote. Ma prima di fare il regalo al nipote ne rivende 65 ad un arabo. A questo punto però si accorge che in questo modo non può più mantenere la promessa fatta al nipote. Qual era il numero minimo di barche che doveva comprare per non mancare alla promessa fatta?
132	L'INVESTIGATORE MATEMATICO	Il vostro compagno di banco scrive un numero di 2 cifre. Voi potete rivolgergli domande alle quali egli deve rispondere esclusivamente con un si o con un no. è possibile con una serie di sei domande scoprire, con certezza, il numero scritto dal compagno? Qual è il numero minimo di domande necessarie per scoprire il numero?
133	LE NOCI DI COCCO	a) Tre marinai trovano un mucchio di noci di cocco. Il primo ne prende la metà più mezza noce. Il secondo prende metà di quello che è rimasto più mezza noce. Anche il terzo prende metà del rimanente più mezza noce. Rimane esattamente una noce che essi danno alla scimmia. Quante erano inizialmente le noci del mucchio? b) Cinque uomini ed una scimmia fecero naufragio su un'isola deserta e passarono il primo giorno a raccogliere noci di cocco per cibo. Poi le ammucchiarono tutte insieme e andarono a dormire. Ma mentre tutti dormivano uno di essi si svegliò e pensando che il mattino dopo vi sarebbero stati dei litigi alla spartizione, decise di prendersi la sua parte. Perciò divise le noci in cinque mucchi. Rimaneva una noce, che egli dette alla scimmia, poi nascose la sua parte e mise tutto il resto assieme. Subito dopo un secondo uomo si svegliò e fece la stessa cosa. Anch'egli dette una noce residua alla scimmia. Uno dopo l'altro tutti e cinque gli uomini fecero la stessa cosa, ognuno prendendo un quinto del mucchio e dando una noce alla scimmia. Alla mattina divisero le noci ed ognuno ottenne lo stesso numero. Naturalmente ognuno sapeva che mancavano delle noci, ma ognuno era colpevole come gli altri e così nessuno parlò. Quante noci c'erano all'inizio? c) E se gli uomini fossero N?	tratto da "Enigmi e giochi matematici" di Martin Gardner
134	I NUMERI CUGINI	Trovare un numero intero tale che spostando la prima cifra dopo l'ultima si ottenga la metà del numero dato. Per esempio si abbia 315, spostando il tre dopo il cinque si ottiene 153 che è vicino ma non è la metà esatta di 315.
135	I QUATTRO BIQUADRATI	È altresì possibile trovare quattro numeri tali che la quarta potenza di uno di essi è pari alla somma delle quarte potenze degli altri tre?
136	Il mistero del numero perfetto dispari	Gli antichi consideravano perfetti certi numeri: sono perfetti i numeri che sono uguali alla somma dei loro divisori. Il numero 6 è un numero perfetto, perché 6 = 1+2+3. Un altro numero perfetto è 28, dato che 28=1+2+4+7+14. lI primo numero perfetto dopo 28 è 496. Ne sono stati trovati altri, e tutti sono pari. Nessuno ha mai trovato un numero perfetto dispari. Ma nessuno è neanche mai riuscito a dimostrare che tutti i numeri perfetti debbano essere per forza pari.
137	UN QUESITO FACILE: I QUATTRO CUBI	Trovare quattro numeri interi tali che il cubo di uno di essi sia uguale alla somma dei cubi degli altri tre.
138	IL NUMERO MANCANTE	Quale è il numero mancante di questa serie? 10, 11, 12, 13, 14, 15, 16, 17, 20, 22, 24, 31, 100,? , 10000
139	LA BATTAGLIA	Dopo una battaglia almeno il 90% perdette un occhio, almeno il 95% perdette un dente, almeno l’80% perdette un braccio e almeno il 75% perdette una gamba. Quanti almeno perdettero tutti e quattro gli organi?
140	NUMERI IN ORDINE	5 2 9 8 4 6 7 3 1 0 Sono i numeri, non in disordine, da 0 a 9. In che ordine sono?
141	UN SIGNORE	Un signore afferma che, stando a casa, un giorno gli è capitato che pur andando a dormire alle otto di sera e essersi svegliato alle sei del mattino del giorno successivo ha dormito per più di 10 ore. E possibile? Perché?
142	LE DUE LANCETTE	Le due lancette di un orologio si sovrappongono perfettamente alle ore 12, dopo quanto tempo saranno di nuovo sovrapposte?
143	LE LANCETTE DI UN OROLOGIO	A partire da mezzogiorno, quante volte, in dodici ore, la lancetta dei minuti (lancetta grande) di un orologio o di una pendola incontrerà quella delle ore (lancetta piccola)?		In dodici ore, la lancetta grande incontra la piccola undici volte e non dodici volte, perché, dopo un giro di quadrante, questa è in anticipo di un dodicesimo di giro
144	QUALCHE CIFRA BIZZARRAMENTE COSTANTE	- Chiedete a una persona di darvi una cifra. Vi darà generalmente la cifra 7. - Chiedetele di dirvi rapidamente un numero di tre cifre identiche. La maggior parte delle volte enuncerà 333. - Chiedete a una persona che non sia un ragioniere quanto fa 1.020 + 1.020; vi risponderà 2.040. - Fatele aggiungere 50, vi darà 2.090. - Dite allora: « Aggiungete 10, quanto fa? ». Vi risponderà quasi invariabilmente 3.000 invece di 2.100. - Facendo valutare delle grandezze (per esempio il numero di piselli che si trovano in una tazzina) da un buon numero di persone, si costata che la maggior parte dei numeri forniti termina con zero. - Poi vengono, per ordine decrescente di frequenza le cifre terminali: 5, 8, 2, 3, 7, 6, 4, 9, 1. Questa curiosa particolarità si ritrova nel Corpus Inscriptionum Latinarum dove figurano le iscrizioni tombali di tre regioni differenti dell’antica Roma. I Romani dell’antichità scrivevano l’età dei morti sulle tombe: ora, l’ordine decrescente di frequenza delle cifre terminali è anche qui: 0, 5, 8, 2, 3, 7, 6, 4, 9, 1.
145	IL PADRE	Una madre ha 21 anni più del suo bambino e fra 6 anni il bambino sarà 5 volte più giovane della mamma. Dov'è il padre?		Il bambino oggi ha X anni e la mamma ha Y anni. Sappiamo che la mamma ha 21 anni più del bambino. Dunque: X + 21 = Y Sappiamo anche che fra 6 anni il bambino sarà 5 volte più giovane della mamma. Quindi possiamo stabilire la seguente equazione: 5 (X + 6) = Y + 6 Sostituiamo adesso la Y con la X e cominciamo a risolvere: 5 (X + 6) = X + 21 + 6 5X + 30 = X + 27 5X - X = 27 - 30 4X = -3 X = -3/4 Il bambino ad oggi ha -3/4 di un anno che è uguale a -9 mesi. IL PADRE È più o meno SULLA MADRE!
146	I 10 sacchetti	Ho dieci sacchetti ognuno con 10 monete ogni moneta pesa 10 grammi a parte un sacchetto in cui le monete pesano 9 grammi con una sola pesata devo individuare il sacchetto che pesa di meno. Ho a disposizione una bilancia con l'ago tipo quella del fruttivendolo come faccio?
147	I LINGOTTI D'ORO	Abbiamo 5 casse contenenti ciascuna lingotti d'oro che hanno tutti lo stesso peso. In un secondo tempo ci si accorge che una delle cinque casse ha tutti lingotti falsi che pesano 11g ciascuno, mentre quelli veri pesano 10g ciascuno. Come individuare, con una sola pesata, qual è la cassa che contiene i lingotti falsi?
148	IL PIONIERE	Siete un pioniere che ha riempito 10 sacchi di pepite d'oro: 1 dei sacchi però contiene pepite false, che pesano 1 gr. di più, ma non sapete quale. Per saperlo dovete pesarle, utilizzando una bilancia elettronica, ma ogni pesata vi costa. Perciò dovrete cercare di impiegare il minor numero possibile di pesate. Sapendo che ogni pepita vera pesa 1 gr. ed ogni pepita falsa pesa 2 gr., qual è il numero minimo di pesate che potrete utilizzare per scoprire il sacco di pepite false? Spiegare il metodo utilizzato
149	IL PROBLEMA DELLE 12 SFERE	Hai 12 sfere, delle quali 11 aventi lo stesso identico peso, mentre 1 è diversa dalle altre. Devi determinare quale delle 12 è quella diversa e il modo in cui è diversa, se cioè è di maggiore o minore peso rispetto alle altre. Per risolvere il quesito hai a disposizione 3 pesate comparative, ossia 3 pesate su una bilancia a 2 piatti.
150	IL PROBLEMA DELLE 12 SFERE	Si ha a disposizione una bilancia a due bracci e dodici palline che sono tutte uguali per forma e dimensione ma in esse una ha peso diverso dalle altre che han peso uguale tra loro. Si chiede di determinare con tre sole pesate quella di peso diverso.		4 e 4 e 4fuori >> 2 e 2 >> 1 e 1
151	LE 7 PALLINE E LA BILANCIA	Ci sono 7 palline che sembrano tutte uguali; in realtà una è più pesante delle altre. Avendo a disposizione una bilancia a due piatti, quante pesate, al minimo, sono necessarie per identificare la pallina più pesante?
152	LE 9 PALLINE E LA BILANCIA	Ci sono 9 palline che sembrano tutte uguali; in realtà una ha un peso diverso dalle altre. Avendo a disposizione una bilancia a due piatti, quante pesate, al minimo, sono necessarie per identificare la pallina di peso diverso determinando se è più leggera o più pesante?
153	LE MONETE FALSE	a) Si ha una bilancia normale (cioè che da direttamente il valore del peso), e 10 pile di 10 monete. Uno dei mucchietti è fatto tutto di monete false, ma non sapete quale; è noto però il peso di una moneta buona e che una moneta falsa pesa un grammo in più del dovuto. Qual è il numero minimo di pesate necessarie a determinare qual è il mucchietto di monete false? b) Si ha una bilancia a due piatti, e 9 monete, una delle quali è leggermente più pesante delle altre. Qual è il numero minimo di pesate per stabilire qual è? c) Sempre con una bilancia a due piatti, si hanno 12 monete, una delle quali è di peso leggermente diverso. Qual è il numero minimo di pesate per stabilire qual è?		a)Con una sola pesata: Metti sulla bilancia: 1 moneta dal primo mucchio, 2 dal secondo, 3 dal terzo .... I peso che ottieni in più del dovuto è relativo al mucchio fatto di monete false. Cioè se per esempio il mucchio pesa 5 g in più del dovuto il mucchio delle monete false è il quinto!
154	LE PALLINE	Ho a disposizione una bilancia a due piatti e possiedo 11 palline,di cui 10 hanno lo stesso peso e 1 è di peso diverso. Qual è il numero minimo di pesate che devo compiere per determinare con esattezza quella pallina con il peso differente?		Se non ricordo male la soluzione è: 3 gruppi da: 1, 5 e 5 prendo 5 e 5 >> se uguali è quella lasciata fuori >> 1 pesata!! altrimenti i 5 più pesanti >> 2 e 2 >> se uguali è quella lasciata fuori >> 2 pesate altrimenti i 2 più pesanti >>1 e 1 >> MAX 3 pesate
155	LE PESATE	Un commerciante ha acquistato 9 lingotti d'oro. Fra questi, però, vi è un lingotto falso che ha un peso minore rispetto agli altri che invece hanno tutti esattamente lo stesso peso. Avendo a disposizione una bilancia a due piatti, quante pesate minimo deve fare il commerciante per scoprire con esattezza qual è il lingotto falso?
156	QUATTRO PALLINE	Si hanno quattro palline che sono uguali nell'aspetto, ma una di esse ha un peso diverso. Si deve individuare questa pallina avendo a disposizione una bilancia a due piatti. Qual è il numero minimo di pesate che occorre effettuare per risolvere il problema.
157	LE CUCITURE	Un pallone di cuoio è ottenuto cucendo venti pezzi di cuoio a forma esagonale e 12 pezzi di cuoio a forma pentagonale. Una cucitura unisce i lati di due pezzi adiacenti. Quale è il numero totale di cuciture
158	LA CONDANNA	Un giudice condanna a morte un prigioniero con questa sentenza: "L'impiccagione avverrà a mezzogiorno in uno dei sette giorni della prossima settimana. Ma lei non saprà in anticipo quale sarà il giorno perché sarà informato solo nella stessa mattinata del giorno fissato per l'esecuzione". Questa affermazione fatta dal giudice contiene un paradosso...Perché?
159	PARADOSSI	a) Se il barbiere del villaggio rade tutti e solo gli uomini che non si radono da soli, chi rade il barbiere? b) Qual è l'essere che cammina ora con 4 zampe, ora con 2 zampe, ora con 3 zampe, che si da il caso che sia meno forte con 4 zampe.
160	LE RELAZIONI DI PARENTELA	In un gruppo di persone erano presenti tutte queste relazioni di parentela: padre, madre, figlio, figlia, fratello, sorella, cugino, nipote maschile, nipote femminile, zio e zia. Qual è il più piccolo gruppo di persone per le quali si può verificare questa circostanza e quali sono i loro rapporti di parentela?
161	I GOLOSONI	Un vassoio è pieno di pasticcini. Passa Andrea e ne mangia la metà più uno; poi passa Bartolomeo e ne mangia la metà più uno; poi passa Cinzia e ne mangia la metà più uno. Quando arriva Davide il vassoio è vuoto. Stabilendo che non si possono spezzare a metà i pasticcini, quanti ce n'erano nel vassoio inizialmente?
162	I PESCI DELLO STAGNO	Un ittiologo voleva stimare il numero di pesci presenti in uno stagno. Buttò quindi una rete con maglie di misura regolare e dopo aver recuperato la rete vi trovò 30 pesci; contrassegnò ogni pesce con un colore opportuno e li rigettò in acqua. Il giorno seguente, usando la stessa rete, catturò 40 pesci e vide che 2 di questi erano contrassegnati. Come calcolò, approssimativamente, il numero dei pesci dello stagno?	Problema molto bello, proposto da H. Steinhaus, Cento problemi di matematica elementare, Boringhieri, 1987. Vale sicuramente una seria riflessione.	Risposta : se N il numero dei pesci nello stagno, supponendo che quelli contrassegnati siano equidistribuiti nello stagno, risulta: 30 :N = 2 :40 ovvero N=600 Osservazione : Nonostante le ipotesi fatte, occorre osservare che il numero di pesci presenti nello stagno può essere molto diverso dal valore N=600 determinato con il metodo descritto, detto della cattura e ricattura. Tale numero rappresenta però la cosiddetta stima di massima verisimiglianza del numero di pesci presenti. (da H.Steinhaus, Cento problemi di matematica elementare, Boringhieri, 1987)
163	GIOCO DI PAROLE	Quanto pesa un oggetto che pesa 1 Kg più della metà del proprio peso?
164	IL NUMERO PI	Il numero che esprime il rapporto fra la circonferenza di un cerchio e il suo diametro. Si scrive generalmente: PI = 3,1416, ma comprende, in realtà, un numero infinito di decimali. Si prende uno spillo e si tracciano su un foglio di carta parecchie parallele distanti, le une dalle altre, del doppio della lunghezza dello spillo. Ciò fatto, si getta lo spillo sulla carta, senza mirare, un grandissimo numero di volte, e si nota se cade su una linea o in un intervallo. Dopo di che si divide il numero dei lanci per il numero delle volte in cui lo spillo è caduto su una linea. Per 100 lanci, si ottiene 2,7; per 500 lanci, 2,94; per 1.000 lanci, 3 all’incirca; per 2.500 lanci, 3,004... e per 10.000 lanci, 3,141, cioè il numero PI con tre decimali. Questi lanci sono indipendenti dalla lunghezza dello spillo.
165	LA RISPOSTA DI PITAGORA	Si racconta che Policrate, tiranno di Samo domandasse un giorno al suo dotto (e scorbutico) suddito di Pitagora quanti alunni frequentassero la sua celebre scuola filosofico-matematica. A quanto si dice, Pitagora gli rispose "Una metà dei miei discepoli studia la geometria, un quarto le leggi della natura, un settimo si occupa di filosofia e tre coltivano la musica. Probabilmente Policrate fece finta di capire e rinunciò alla sua curiosità. Vediamo, invece, se noi riusciamo a interpretare la sibillina risposta di Pitagora. Gli alunni che studiavano geometria, scienze e filosofia erano 1/2+1/4+1/7=25/28 del totale. La frazione complementare di 25/28 è 3/28; dunque i tre studenti di musica erano i 3/28 di tutto il gruppo.
166	IL CACCIATORE E L'ORSO	Un cacciatore di orsi parte per una battuta di caccia. Raggiunto il luogo desiderato pianta la sua tenda e prepara tutte le sue cose. Si incammina verso Sud per un chilometro alla ricerca di orsi, ma non trova nulla. Decide perciò di deviare percorrendo un chilometro verso Est. Di nuovo non trova nulla e si dirige ora verso Nord. Dopo un chilometro trova un orso che sta frugando proprio nella tenda che lui aveva piantato poco prima; lo agguanta con la sua rete e lo cattura. Di che colore è l'orso e perché è certamente di quel colore?
167	IL PONTE DEGLI U2	Il complesso degli U2 sta per fare un concerto a Dublino. Mancano 17 minuti all'inizio del concerto ma, per raggiungere il palco, i membri del gruppo devono attraversare un piccolo ponte che è tutto al buio, disponendo di una sola torcia elettrica. Sul ponte non possono andare più di due persone per volta. La torcia è essenziale per l'attraversamento, per cui deve essere portava avanti e indietro (non può essere lanciata da una parte all'altra) per consentire a tutti di passare. E tutti sono dalla stessa parte del ponte. Ciascun componente del complesso cammina a una velocità diversa. I tempi individuali per attraversare il ponte sono: - Bono, 1 minuto - Edge, 2 minuti - Adam, 5 minuti - Larry, 10 minuti Se attraversano in due, la coppia camminerà alla velocità del più lento. Ad esempio: se Bono e Larry attraversano per primi, quando arrivano dall'altra parte saranno trascorsi 10 minuti. Se Larry torna indietro con la torcia saranno passati altri dieci minuti, per cui la missione sarà fallita. La risposta al test non prevede alcun "trucco". Si tratta solo di indicare lo spostamento delle persone nell'ordine corretto.	Si tratta di uno dei test utilizzati nella selezione del personale della Microsoft. Si racconta che c'è chi lo ha risolto in 3 soli minuti, mentre qualcun altro ha trovato la soluzione utilizzando un programma in linguaggio C, ma impiegando ben 37 minuti. Il tempo indicato dalla Microsoft per risolverlo, tuttavia, è di soli 5 minuti !! Alla Motorola, tra 50 candidati nessuno è riuscito a risolverlo. Esistono due possibili soluzioni.	Fanno un primo viaggio i due più veloci: 2 minuti. Torna con la torcia, ad esempio, il più veloce: + 1 minuto (=3). Fanno un secondo viaggio i due più lenti: + 10 minuti (=13). Torna con la torcia l'altro veloce rimasto al di là: + 2 minuti (=15). Fanno l'ultimo viaggio i due più veloci: + 2 minuti (=17)
168	UN GIOCO DI PRESTIGIO BASATO SUL NOVE	Il facile metodo usato per sommare un numero composto solo di 9 è la base di molti giochi con i numeri. Chiedete a un amico di scrivere un numero di quattro cifre: 6.921 ad un altro di scrivere ancora un numero con quattro cifre: 4.317 Voi scrivete: 5.682 Chiedete di nuovo di scrivere un numero di quattro cifre: 8.692 Voi scrivete: 1.307 Prima dì chiedere a qualcuno di fare la somma, scrivete la soluzione, 26.919, sul rovescio di un foglio di carta. Fate calcolare a ciascuno il totale, rovesciate il vostro foglio con la risposta che risulterà esatta con sorpresa dei presenti: si domanderanno certo come avete fatto per scrivere il risultato così in fretta.
169	25 PALLINE BIANCHE E 25 PALLINE NERE	Abbiamo 2 scatoloni, 25 palline bianche e 25 palline nere. Le 50 palline vanno distribuite tra i due scatoloni in modo da avere la massima probabilità che venga pescata, da uno scatolone scelto a caso, una pallina bianca. Come vanno distribuite le palline?		In uno scatolone metteremo una sola pallina, bianca. Nel secondo scatolone tutte le altre. Otterremo il 100% su uno scatolone e quasi il 50% sull'altro.
170	I TRE SCATOLONI	Ci sono tre scatoloni; il primo contiene due palline bianche, il secondo due palline nere ed il terzo una bianca e una nera. Sui rispettivi coperchi ci sono le scritte BB, NN e BN ma i coperchi sono messi in disordine in modo tale che quello che c’è scritto sul coperchio sicuramente non coincide con quanto contenuto all’interno dello scatolone. Quante palline è necessario estrarre, al minimo, per determinare l’esatto contenuto dei tre scatoloni?
171	DUELLO A TRE	Una mattina il signor Neri, il signor Rossi e il signor Bianchi decidono di risolvere un conflitto duellando con le pistole, finché uno solo di loro sopravviva. Il signor Neri è il peggior tiratore e in media colpisce il bersaglio solo una volta su tre. Il signor Rossi è più bravo e colpisce il bersaglio due volte su tre. Il signor Bianchi è il migliore di tutti e colpisce sempre il bersaglio. Per rendere più equo il duello a tre, al Signor Neri è concesso di sparare per primo, al signor Rossi (se sarà ancora vivo) di sparare per secondo e al signor Bianchi (purché sia ancora vivo) di sparare per terzo. Il giro si ripeterà in quest'ordine finché uno solo resti vivo. La domanda è: c'è un avversario contro il quale è più conveniente che spari il signor Neri?	Proposto da Simon Singh, nel suo libro L'ultimo teorema di Fermat, un bel libro in cui si racconta la storia del celebre teorema, fino alla sua recente dimostrazione.
172	I TRE PISTOLERI	Ci sono 3 pistoleri: A, B, C. A uccide con probabilità 30% B con 50% C con il 100%. Iniziano la sfida: prima A, poi B, poi C, poi A... finchè solo uno di loro resterà vivo. Si chiede di stabilire qual è la probabilità di sopravvivenza di ognuno posto che ciascuno prenda la decisione che massimizzi la sua probabilità di sopravvivenza.
173	GIOCO A PREMI	Supponiamo di essere a un gioco a premi e di dovere scegliere quale porta aprire fra le tre proposte dal presentatore. Dietro una di queste c'è un'auto, nelle altre due... una capra. Noi scegliamo una porta, e come capita in tutte le puntate, il presentatore ci dice "Ne sei proprio sicuro? Puoi ancora cambiare la scelta: anzi, ti voglio aiutare", e apre una delle porte che noi non abbiamo scelto, mostrando una capra. Ammesso che vogliamo vincere l'auto, ci conviene cambiare porta, o la cosa è indifferente?
174	IL TESTIMONE	Un taxi di Combicity viene coinvolto in un incidente e poi si allontana senza prestare soccorso. Ma un testimone ha assistito alla scena, avvenuta di notte, e dichiara che il taxi era blu. La polizia che indaga e che ha interrogato il testimone, verifica con lui, alla stessa ora della notte, la correttezza delle sue identificazioni dei taxi e rileva che riesce a identificare il colore esatto soltanto nell'80% dei casi, sbagliando quindi il colore dei taxi nel 20% dei casi. Inoltre la polizia sa che i taxi di Combicity sono per l'85% blu e per il 15% gialli. Qual è la probabilità che il taxi coinvolto nell'incidente sia realmente blu? E nel caso in cui il testimone avesse dichiarato che il taxi era di colore giallo, sempre con un'affidabilità all'80%, quale sarebbe stata la probabilità che il taxi coinvolto fosse realmente giallo?
175	UN PROFESSORE	Un professore ha una scatola di 1300 penne, e vuole distribuirle in modo equo ai suoi alunni. Così incomincia col dare ad ognuno tante penne quanti ne sono gli alunni. Dopo di che, visto che ne rimangono ancora un bel po', decide di darne altre due ciascuno. Alla fine nella scatola ne rimangono solo cinque, che egli tiene per sé. Quanti sono gli alunni?
176	UN FOGLIO DI CARTA	Immaginate di avere un foglio di carta rettangolare spesso un decimo di millimetro e sufficientemente grande. Ora piegatelo a metà in modo da ottenere due mezzi fogli sovrapposti, quindi con uno spessore doppio. Continuate poi a piegare in due, ottenendo via via fogli sempre più piccoli e spessori maggiori. Dopo 42 piegamenti, immaginate di salire sulla torre di carta che avete creato. Secondo voi di quanto vi potete innalzare? 1) Riuscite appena a fare uno scalino (circa 20 cm) 2) Arrivate al primo piano di una casa (circa 3 m) 3) Potete conquistare la cima dell'Everest (circa 8800 m) 4) Sarete il primo piegatore di carta sulla Luna (circa 385000 km) P.S.: 42 non è un numero casuale, infatti è la Risposta alla Domanda Fondamentale sulla Vita, l'Universo e Tutto quanto (v. Adams, Douglas). Usato come risposta standard nel caso non si sappia o non si voglia rispondere o come numero non-casuale.
177	LA NINFEA	Una ninfea cade in un lago. Ogni giorno raddoppia la sua superficie e in 100 giorni copre tutta la superficie del lago. Quanti giorni ha impiegato per coprire la metà del lago?
178	LE RANE SPECIALI	Ci sono delle rane, speciali, che ogni giorno raddoppiano il proprio volume. Una di esse, buttata in un pozzo appena nata, in 20 giorni ha riempito completamente il pozzo. Dopo quanti giorni il pozzo sarebbe stato pieno se le rane fossero state due?
179	IL PROBLEMA DELLA CARTA PIEGATA	«Signori», dite nel tono più ingenuo possibile cominciando a piegare in due negligentemente un foglio di carta piuttosto sottile, « voi vedete che quello che faccio non è molto complicato: io piego semplicemente in due questo foglio di carta assolutamente ordinario. Poi, lo piego ancora una volta in due (lo si fa in senso perpendicolare alla prima piegatura), ancora una volta in due, e così di seguito. Voi vedete che non è cosa lunga né difficile (vi siete fermati, sempre parlando, alla quarta piegatura): è questione di un secondo per fare ogni piegatura, non è vero? Se lo facessi, mettiamo cinquanta volte di seguito (parlando, si è lentamente, e senza darvi importanza, spiegato il foglio), occorrerebbe dunque un minuto, non più. «Ebbene, supponete che io lo faccia cinquanta volte — ma non voglio farvi perdere un minuto a starmi a guardare — quale spessore, pressa poco, avrebbe il quadernetto così formato in meno d’un minuto, supponendo che questo foglio di carta abbia un decimo di millimetro di spessore. Naturalmente, non tengo conto dell’aria interposta se i fogli non sono assolutamente aderenti».		112.589.990 chilometri 674 metri 262 millimetri. Si ha, infatti, 2 alla 50 potenza
180	IL PROBLEMA DEI CHICCHI DI GRANO	Secondo la leggenda o la storia, a Sessa che aveva inventato gli scacchi, il re di Persia, incantato da quel gioco, chiese che esprimesse un desiderio. Era pronto, disse, a offrirgli una parte del suo regno. Con aria modesta, l’astuto matematico chiese un chicco di grano per la prima delle 64 caselle della sua scacchiera, 2 chicchi per la seconda, 4 per la terza, 8 per la quarta, e così di seguito, raddoppiando ad ogni casella, fino all’ultima. I cortigiani trovarono che era stupido domandare così poco, quando gli si offrivano delle ricchezze. Ma Sessa mostrò che il re, per quanto ricco fosse, non avrebbe potuto soddisfare la sua richiesta.
181	IL PROBLEMA DEI DUE NENUFERI	Un nenufero tropicale, a crescenza estremamente rapida, ingrandisce in modo tale che ogni giorno copre una superficie doppia di quella che occupava la vigilia, così che copre interamente, al termine del trentesimo giorno, il bacino nel quale si trova. Quanto tempo ci metteranno per ricoprire il medesimo bacino due nenuferi della medesima superficie in origine e del medesimo sviluppo?
182	L'AMEBA	In un bicchiere viene messa un'ameba che esattamente dopo un secondo forma un altro organismo uguale a se stesso. Dopo circa un'ora si riempie metà bicchiere. Quanto tempo occorrerà per riempire tutto il bicchiere?
183	IL PARADOSSO DI PROTAGORA	Si narra che Protagora (nato ad Abdera verso il 485 a.c; insieme a Gorgia fu il maggior filosofo Sofista) avesse tra le altre cose insegnato legge ad uno studente di nome Euatlo. Essendo questi povero, i due rimasero d'accordo che Euatlo avrebbe ricompensato Protagora non appena avesse vinto la sua prima causa. Terminati che ebbe gli studi di retorica e diritto, Euatlo decise di seguire la carriera politica, abbandonando così il proposito di praticare la professione legale. Protagora, che ancora doveva essere pagato dell'onorario pattuito, sollecitò a Euatlo il pagamento. Ma Euatlo rispose che avrebbe dovuto pagarlo solo dopo che avesse vinto la sua prima causa (come da accordi) e ciò non era ancora avvenuto. Allora Protagora, irritato decisamente per la decisione presa dal suo ex allievo, decise di citare Euatlo in giudizio per fargli mantenere la promessa. Di fronte alla corte, Protagora argomentò così le sue tesi: se Euatlo avesse perso la causa, allora avrebbe dovuto obbedire al giudizio della corte e quindi pagare il dovuto; viceversa, sempre secondo Protagora, se Euatlo avesse vinto, allora avrebbe appunto vinto la sua PRIMA causa ed indi, visti i termini del vecchio accordo, avrebbe dovuto versare a Protagora il compenso pattuito. Viceversa, Euatlo, in maniera altrettanto impeccabile, argomentò così le sue ragioni: se avesse vinto la causa, la corte avrebbe dato ragione a lui, quindi non avrebbe dovuto nulla a Protagora. D'altronde, secondo il punto di vista di Euatlo, se avesse perso la causa anche in questo caso non avrebbe dovuto pagare il suo vecchio Maestro non avendo infatti ancora vinto la sua prima causa. Qual è il ragionamento più corretto? Quello di Euatlo o di Protagora?
184	IL PODERE QUADRATO DELL'AGRICOLTORE	Un agricoltore possedeva un appezzamento di terreno di forma quadrata. Ad ogni vertice del quadrato era situato un albero che non gli apparteneva. Se l'agricoltore avesse voluto raddoppiare la sua proprietà senza toccare gli alberi, lasciandone invariata la forma, come avrebbe dovuto fare?
185	I CAMMELLI IN EREDITÀ	Uno sceicco, morendo, lascia in eredità ai suoi tre figli 17 cammelli con l’ordine che vengano divisi nel seguente modo: – 1/2 al primogenito – 1/3 al secondogenito – 1/9 al terzo. I tre eredi, in difficoltà per la divisione, si rivolsero ad un saggio che disse: "Vi presto io un cammello e così ora i cammelli sono 18; a questo punto la divisione è facile: 9 cammelli al primo figlio, 6 al secondo e 2 al terzo; così avete tutti avuto un po’ di più e visto che 9 + 6 + 2 = 17, io posso riprendermi il mio!" Com’è possibile?
186	I RESTI SUCCESSIVI	Qual è il numero più piccolo che, diviso per 10, dà 9 per resto, diviso per 9 dà 8 per resto, diviso per 8 dà 7 per resto, diviso per 7 dà 6 per resto...,diviso per 2 dà 1 per resto?
187	Indovina il numero	Qual è quel numero che diviso per 3 dà resto 1, diviso per 5 dà resto 2 e diviso per 7 dà resto 3? E quanti se ne possono trovare almeno tra diciamo i primi 5000 numeri naturali?
188	8 REGINE	È possibile mettere 8 regine su una scacchiera senza che, con le normali regole del gioco degli scacchi, si diano scacco l'un l'altra ? Naturalmente si. Come?
189	LA SCACCHIERA MUTILATA	I materiali per questo problema sono una scacchiera e 32 pezzi di domino. Ogni pezzo di domino è di dimensioni tali da coprire esattamente due quadrati adiacenti della scacchiera. Perciò i 32 pezzi possono coprire tutte le 64 caselle della scacchiera. Supponiamo ora di eliminare le due caselle sistemate agli angoli opposti di una diagonale e di eliminare un pezzo di domino. È possibile sistemare i 31 pezzi rimanenti sulla scacchiera in modo da coprire i rimanenti 62 quadretti? Se sì, mostrare come si può fare; se no, dimostrare l'impossibilità.	tratto da "Enigmi e giochi matematici" di Martin Gardner
190	UN CAVALLO SU UNA SCACCHIERA	Il cavallo su una scacchiera si muove ad L (due caselle in verticale e una in orizzontale, oppure due caselle in orizzontale e una in verticale). Partendo da una casella qualsiasi è possibile muovere il cavallo, facendogli toccare tutte e 64 le caselle della scacchiera, riportandolo alla casella di partenza.
191	SCIOGLILINGUA	• Chi troppo in alto sal cade sovente precipitevolissimevolmente • Ciò che è, è; ciò che non è, non è; ciò che è, non è ciò che non è; ciò che non è, non è ciò che è. • Dietro a quel palazzo c'é un povero cane pazzo. Date un pezzo di pane a quel povero pazzo cane. • Eva dava l'uva ad Ava; Ava dava l'uova ad Eva; ora Eva è priva d'uva, mentre Ava è priva d'uova. • Figlia, sfoglia la foglia; sfoglia la foglia, figlia. • Se l'arcivescovo di costantinopoli si disarcivescovisconstantinopolizzasse, ti disarcivescoviscontantinopolizzeresti tu? • Sopra la panca la capra campa, sotto la panca la capra crepa. • Sul tagliere l'aglio taglia. Non tagliare la tovaglia. La tovaglia non é aglio. Se la tagli fai uno sbaglio. • Tre tigri contro tre tigri, tre tigri contro tre tigri, tre tigri contro tre tigri, tre tigri contro tre tigri..... • Trentatre trentini entrarono trotterellando in Trento, tutti e trentatre trotterellando. • Uattanciu, uattan scheditten, i sbidelin uotten totten, acchendo achelitten bitten. (by Gianni Benassi...dovrebbe significare..."stai attento!")
192	SERIE	1 11 21 1211 111221 312211 13112221 1113213211 Qual è la prossima riga?
193	IL BARBONE	Un barbone raccoglie mozziconi di sigaretta e mettendone assieme 4 si costruisce una sigaretta (quasi) nuova. Se riesce a fumare 7 sigarette (quasi) nuove, qual è il numero minimo di mozziconi che deve aver trovato e quanti gliene rimangono alla fine?
194	IL POVERO SOLDATO	Un povero soldato deve far saltare un ponte dopo 45 minuti esatti. Purtroppo non ha nessun modo di poter determinare il trascorrere del tempo tranne 2 micce che durano esattamente 1 ora ciascuna. Sfortunatamente le due micce non hanno una combustione lineare, cioè il tempo di combustione non è proporzionale alla lunghezza; così metà miccia non brucia in mezz'ora. Come può comunque riuscire nel suo l'intento?		La soluzione si basa sull'osservare che una miccia accesa da entrambi gli estremi si consuma esattamente in mezz'ora; la combustione non lineare fa sì che le scintille provenienti dai due estremi non si incontrino a metà della miccia ma l'incontro avverrà comunque dopo mezz'ora. A questo punto il buon soldato accende una miccia da entrambi i lati e l'altra da un lato solo. Quando la prima sarà consumata sarà passata mezz'ora e mezz'ora sarà la durata residua della seconda miccia. Accendendo ora la seconda miccia - da mezz'ora - anche dall'altro estremo questa si consumerà in 15 minuti; 15 minuti che, sommati alla prima mezz'ora, fanno i 45 minuti cercati.
195	UNA SFERA LISCIA	Immagina di essere su di una sfera perfettamente liscia, grande quanto il Sole. Una fascia di metallo è stretta attorno all'equatore. Ora supponi di allungare di un metro la fascia in modo che si sollevi dalla superficie uniformemente attorno alla sfera. Adesso prendi un'altra sfera perfettamente liscia, grande però quanto un'arancia, anch'essa con una fascia di metallo stretta attorno al suo equatore. Supponi di allungare di un metro la fascia, in modo che si sollevi dalla superficie uniformemente attorno alla sfera. In quale dei due casi lo spazio creatosi fra la superficie della sfera e la fascia metallica sarà sufficiente per farci passare una pallina da tennis?
196	NELLA STALLA	In una stalla vi sono oche e conigli. Contando le teste sono 32, contando le zampe sono 100. Quante sono le oche e quanti i conigli.		C=18, O=14
197	PROBLEMA DELLA PEZZA DI STOFFA	Un sarto possiede una pezza di stoffa di 18 m; ne taglia 2 m al giorno. In capo a quanti giorni avrà tagliato tutta la stoffa?		alla fine del 29esimo giorno
198	LA SERIE	Continua la serie 1 1 2 3 5 8 13 21... Dare due risposte (una facile e una difficile) e giustificarle.
199	SUCCESSIONE	Come prosegue la successione 2,12,1112,3112,132112,...? In questa successione non possono esserci altre cifre oltre a 1, 2 e 3, come si può dimostrare?
200	SUCCESSIONE DI NUMERI	Qual è il termine successivo in questa successione? 1 - 11 - 21 - 1211 - 111221 -…
201	UNO STRANO TEST DI FISICA	In una liceo di una grande città ci sono due sezioni di cinque classi ciascuna; ogni classe è di venti studenti. Gli alunni della sezione A sono molto bravi e diligenti mentre quelli della B sono sfaticati ed ignoranti. Il più bravo degli studenti è Benedetti mentre il più somaro è Scarpa. Nella sezione A insegnano il Prof. Rossi di matematica e fisica; il Prof. Verdi di italiano e latino; Bianchi di storia e filosofia; Smith di inglese. Nella sezione B insegnano Neri di matematica e fisica; Marroni di italiano e latino; Violetti di storia e filosofia; Brown di inglese. Il preside è il Prof. Paolucci. Ci sono poi tre bidelli, Mario, Pino e Anna. Un giorno il Prof. Rossi decide di far svolgere un test di fisica a tutti gli studenti per verificare le loro conoscenze; siccome il professore è un po' un mattacchione decide di far fare il test anche a tutti i colleghi, il preside ed i bidelli, tanto per avere una controprova! Il test si compone di dieci domande del tipo VERO/FALSO su vari argomenti di fisica; per ogni risposta esatta si ottiene un punto; per ogni risposta sbagliata si ottengono zero punti. Dopo aver fatto il test il professore analizza i risultati e scopre che i ragazzi della sezione A sono andati in genere meglio di quelli della B. I colleghi professori ed i bidelli sono andati in genere così così. Ci sono comunque molte valutazioni sul cinque, sei e sette. Quello che colpisce il professore è che c'è un solo compito con votazione dieci ed uno solo con votazione zero. Il professore riconosce subito quello con votazione dieci che è quello che lui stesso ha svolto. Chi ha svolto il compito con valutazione zero ?
202	IN UN PICCOLO PAESE	In un piccolo paese esistono soltanto giovani coppie, senza bambini, che apparentemente conducono un'esistenza tranquilla. Una domenica mattina il parroco, durante la messa, dice ai fedeli: - "In questo paese esiste almeno una donna che tradisce il proprio marito. Inoltre io so che tutti i mariti conoscono la storia delle altre mogli, ma non della propria. Io invito ogni marito che scopra il tradimento della moglie a presentarsi nel mio ufficio alla mezzanotte del giorno in cui scopre il tradimento, per discutere il problema". - I giorni passano tranquilli senza che nessun marito si presenti al parroco. Improvvisamente, a mezzanotte del decimo giorno, tutti i mariti traditi si precipitano contemporaneamente dal parroco. Quanti erano, e come hanno fatto ad avere la certezza del tradimento della propria moglie?		- Se fosse una sola moglie a tradire, tutti i mariti saprebbero quale è la moglie traditrice mentre il solo marito tradito non lo sa. Ma quando il parroco dice che c'è almeno una moglie che tradisce e lui sa che tutte le altre mogli non tradiscono automaticamente diventa certo che sia la propria moglie! - Se fossero 2 mogli a tradire, appena il parroco parla tutti i mariti sanno che ci sono 2 mogli traditrici eccetto i rispettivi mariti (che indico con A e B). Infatti il marito A sa solo della moglie di B e il marito B della moglie di A. Ma dopo il primo giorno che nessuno va dal parroco, si rendono conto che ci sono almeno 2 mogli che tradiscono e quindi sia il marito A e il Marito B capiscono che sono le proprie mogli.  - Se fossero 3 mogli traditrici, allo stesso modo il 1° e il 2° giorno, e fino a quasi alla fine del terzo giorno dato che nessuno va dal parroco, i 3 mariti conoscono le due 2 mogli di altri traditrici ma appena scatta mezzanotte del 3° giorno si rendono conto che di mogli ne sono 3 quindi anche la propria. - E così via... - Se fossero 10 mogli, ci vogliono 10 giorni, e quindi le mogli traditrici erano 10.H200
203	I TRIANGOLI DI ALICE	"Ieri notte sono stato sveglio sino alle 4 di mattina, per questo provocante problema, mandatomi da New York: trovare tre triangoli rettangoli (uguali in area) con lati espressi da numeri razionali. Ne ho trovati due, i cui lati sono 20, 21, 29 e 12, 35, 37; ma non sono riuscito a trovarne tre." Il problema è stato ripreso da Martin Gardner, il grande esperto in giochi matematici, il quale osserva che esistono infinite soluzioni, anche per un numero di triangoli superiore a tre, ma in questo caso, le superfici hanno valori non inferiori a numeri di sei cifre. "Nel caso di tre triangoli esiste tuttavia una soluzione - dice Gardner - in cui l'area è inferiore a 1000 e i tre triangoli hanno lati con numeri interi". Qual è questa soluzione?	Lewis Carroll, l'autore di Alice nel Paese delle Meraviglie, scriveva sul suo diario, il 19 dicembre 1898
204	TURISTI A ROMA	Tre turisti, Bill, Gary e Paul si trovano a Roma in tre alberghi diversi, Eden, Plaza e Farnese, in tre camere di numero diverso 124, 142 e 226. Il turista alloggiato all'Eden ha lasciato la sua camera, la 142, per una passeggiata fino a Piazza di Spagna dove incontra Gary che alloggia al Plaza. Paul si trova invece nella sua camera, la 226, e sta facendo una doccia. Trovare il nome dell'albergo e il numero della camera dei tre turisti.
205	IN UNA CAMPAGNA	In una campagna vi è un gran numero di uccelli (non importa quanti, ma molti) appartenenti a tre specie diverse. Devono sistemarsi su un albero che conta in tutto 8 rami. Sapendo che ogni ramo può essere occupato da un solo uccello, quante combinazioni di specie di uccelli si possono avere sull'albero, tenendo anche presente che sull'albero devono esserci almeno due specie diverse?
206	RESTO ZERO	Una contadina porta delle uova al mercato. Sa che contandole a 2 a 2 ne avanza 1, contandole a 3 a 3 ne avanza 1, a 4 a 4 ne avanza 1, a 5 a 5 ne avanza 1, a 6 a 6 ne avanza sempre 1 mentre contandole a 7 a 7 non ne avanza alcuna, ha un numero esatto. Quante uova ha la contadina?	Liber Abaci di Leonardo Fibonacci.
207	IN AUTOSTRADA	Percorrendo un tratto autostradale alla velocità costante di 120 km/h, un automobilista sorpassa, in 30 minuti, 50 camion che a loro volta marciano a una velocità di 80 km/h. Ora, supponendo costanti tutte le velocità in gioco e soprattutto mantenendo costanti i flussi di traffico, quanti camion percorrono quell'autostrada in un'ora? In poche parole un'ipotetica persona ferma al lato della strada quanti camion vedrebbe passare davanti a sé in un'ora?		Passano 200 camion ogni ora. L'automobilista ha velocità relativa rispetto ai camion di 40 km/h >> In mezz'ora, percorre 20 km, rispetto ai camion. In un tratto di strada lungo 20 km, ci sono 50 camion >> ogni camion dista dal successivo 400 m (=20km/50) >> tra il passaggio di un camion e l'altro, passano 18 secondi (=0,400/80=0,005 ore) >> in 1 ora ne passano 200 (=3600/18).
208	IL CICLISTA	Un ciclista scala una montagna alla media di 20 km/h , e poi, giunto in cima, gira la bicicletta e ridiscende a valle (seguendo la stessa strada) ad una media di 60 km/h. Qual è la media complessiva tenuta dal ciclista, durante tutto il suo viaggio?	tratto da "Matematica dell'incertezza" di Giuliano Spirito	Per il 31) con a e b i tempi di andate e di ritorno. S=a*20 S=b*60 V=2S/(a+b) V=2S/(S/20+S/60) V=2S/(S*(1/20+1/60) V=2/(4/60)=30km/h
209	CHI MENTE E CHI DICE IL VERO	"In questi ultimi giorni ho lavorato molto ad una serie di curiosi problemi su affermazioni vere o false. Ad esempio, A dice che B mente; B dice che C mente; C dice che A e B mentono". La domanda è: chi mente e chi dice la verità?	Problema di Lewis Carroll, ripescato dal suo celebre diario, alla data del 27 maggio 1894.
210	VERO E FALSO	Siamo a un bivio senza indicazioni e non sappiamo da che parte andare. Una strada porta a Verano, un paese i cui abitanti dicono sempre la verità, e l'altra a Falsago, un paese i cui abitanti mentono sempre. Al bivio incontriamo un uomo che non sappiamo se sia di Verano o di Falsago. Noi vogliamo raggiungere Verano e possiamo fare una sola domanda all'uomo che abbiamo incontrato. Che cosa gli dobbiamo chiedere per essere sicuri di scoprire la direzione per Verano?		Sol:1) "Mi indichi la strada per il tuo paese?" Se è di Verano, indica Verano. Se è di Falsago indicherà Verano. Sol2) "E' questa la strada che porta al tuo villaggio ?" se la risposta e' SI la strada porta al villaggio Verano, se la risposta e' NO porta al villaggio Falsago.
211	IL SINDACO	Il sindaco di un comune compra un certo numero di alberi e decide di farli piantare ai lati delle vie della sua città. Così pensa di piantare per ogni via tante piante quante sono le stesse vie. Per questo scopo però servono altre 175 piante che egli subito ordina. Alla fine ogni via avrà esattamente un trentesimo del numero delle piante comprate inizialmente. Quante sono le vie della città?
212	IL VOLO ATTORNO AL MONDO	Un gruppo di aerei è dislocato su una piccola isola. Il serbatoio di ogni aereo contiene esattamente carburante sufficiente a consentirgli mezzo giro del mondo, ma è possibile trasferire quanto carburante si vuole dal serbatoio di un aereo a quello di un altro mentre gli aerei sono in volo. La sola fonte di carburante è sull'isola e si suppone che non venga perduto tempo nel rifornimento sia in aria che al suolo. Qual è il numero minimo di aerei necessario per assicurare il volo di uno di essi per un giro completo attorno al mondo, ammettendo che gli aerei abbiano la stessa velocità costante rispetto al suolo, lo stesso consumo di carburante e che tutti gli aerei rientrino sani e salvi alla base?	Tratto da "Enigmi e giochi matematici" di Martin Gardner
213	LA SOMMA DEI NUMERI	Calcolare la somma di tutti i numeri interi da 1 fino a 100. Questo problema venne assegnato dal maestro a Carlo Federico Gauss (grande matematico ed astronomo tedesco, nato a Brunswik nel 1777 e morto a Gottingen nel 1855) quando questi non aveva che nove anni. Il compito era appena dettato che, con grande meraviglia dell'insegnante, Gauss alzò la mano e rispose immediatamente: 5050. Non è possibile — disse il maestro — che in così poco tempo, e a memoria, tu possa aver sommato cento numeri! Tu sapevi già il risultato in precedenza. No, non lo sapevo — rispose calmo lo scolaretto — il calcolo è semplicissimo: se io sommo ogni numero da 1 a 49 con i numeri corrispondenti, disposti in ordine decrescente, da 99 a 51 ottengo sempre 100 e quindi, in totale, 4900. Rimangono esclusi i numeri 50 e 100 che, aggiunti alla somma precedente, danno appunto 5050.
214	L'EUROBIRBO	Un cassiere di banca distratto scambia centesimi per euro nel pagarti un assegno, dandoti euro per la cifra dei centesimi e centesimi per la cifra degli euro. Dopo aver acquistato un giornale da cinque centesimi, ti accorgi che ti è rimasto esattamente il doppio dell'assegno iniziale. Quant'era l'ammontare dell'assegno?
215	LO SCAVO	Un campo quadrato di lato L è attraversato a una certa profondità da un tubo del metano perfettamente rettilineo. Peccato che non si sappia dove passa e si deve quindi fare uno scavo per individuarlo. Si chiede di beccare il tubo con lo scavo più corto. (es. se si scavasse lungo tutto il perimetro (4L) si sarebbe sicuri di trovarlo, ma basterebbe scavare lungo 3 lati (3L) per ottenere lo stesso risultato... ovviamente basta ancora meno...)
216	UNA VECCHIETTA	Una vecchietta con un canestro pieno di mele va bussando per le case per venderle. Alla signora della prima casa vende la metà delle mele del canestrino + mezza mela. Alla quella della seconda casa vende la metà delle mele rimaste nel canestrino + mezza mela. Infine a quella della terza casa vende la metà delle mele rimaste nel canestrino + mezza mela. A questo punto il canestro è vuoto. Quante mele c’erano nel canestro all’inizio?